Page 83 - Dynamic Loading and Design of Structures

Page 61

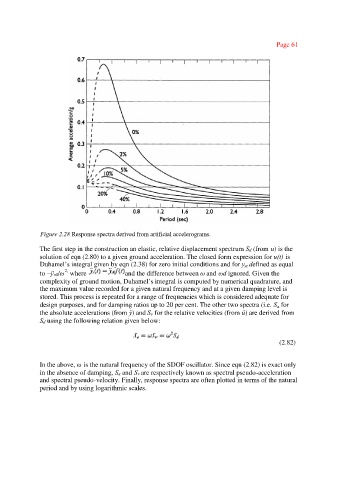
Figure 2.28 Response spectra derived from artificial accelerograms.

The first step in the construction an elastic, relative displacement spectrum Sd (from u) is the
solution of eqn (2.80) to a given ground acceleration. The closed form expression for u(t) is
Duhamel’s integral given by eqn (2.38) for zero initial conditions and for y defined as equal
st
2,
to −s0/ω where and the difference between ωand ωd ignored. Given the
ÿ
complexity of ground motion, Duhamel’s integral is computed by numerical quadrature, and
the maximum value recorded for a given natural frequency and at a given damping level is
stored. This process is repeated for a range of frequencies which is considered adequate for
design purposes, and for damping ratios up to 20 per cent. The other two spectra (i.e. S for
a
the absolute accelerations (from ÿ) and Sv for the relative velocities (from ůare derived from
)
Sd using the following relation given below:

(2.82)

In the above, ωis the natural frequency of the SDOF oscillator. Since eqn (2.82) is exact only
in the absence of damping, Sa and Sv are respectively known as spectral pseudo-acceleration
and spectral pseudo-velocity. Finally, response spectra are often plotted in terms of the natural
period and by using logarithmic scales.