Page 262 - Dynamics and Control of Nuclear Reactors

APPENDIX C Basic reactor physics 263

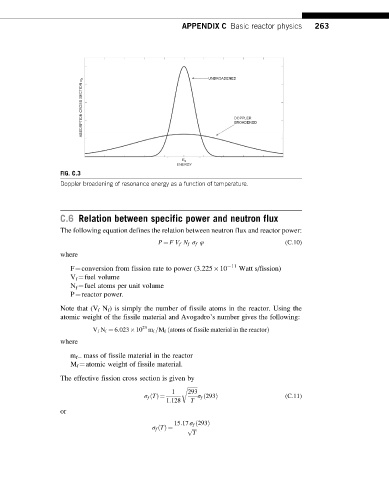
ABSORPTION CROSS SECTION s a UNBROADENED DOPPLER

BROADENED

E 0
ENERGY
FIG. C.3
Doppler broadening of resonance energy as a function of temperature.

C.6 Relation between specific power and neutron flux
The following equation defines the relation between neutron flux and reactor power:
P ¼ FV f N f σ f φ (C.10)

where
F¼conversion from fission rate to power (3.225 10 11 Watt s/fission)
V f ¼fuel volume
N f ¼fuel atoms per unit volume
P¼reactor power.

Note that (V f N f ) is simply the number of fissile atoms in the reactor. Using the
atomic weight of the fissile material and Avogadro’s number gives the following:
23
ð
V f N f ¼ 6:023 10 m f =M f atoms of fissile material in the reactorÞ
where
m f¼ mass of fissile material in the reactor
M f ¼atomic weight of fissile material.
The effective fission cross section is given by
r ffiffiffiffiffiffiffiffi
1 293
σ f TðÞ ¼ σ f 293ð Þ (C.11)
1:128 T
or
ð
15:17 σ f 293Þ
σ f TðÞ ¼ p ffiffiffi
T