Page 56 - Dynamics and Control of Nuclear Reactors

4.8 The inhour equation 47

5
5 s loop time
7.5 s loop time
4

P/P(0) 3

2

1
0 5 10 15 20 25 30 35 40 45 50
Time (s)
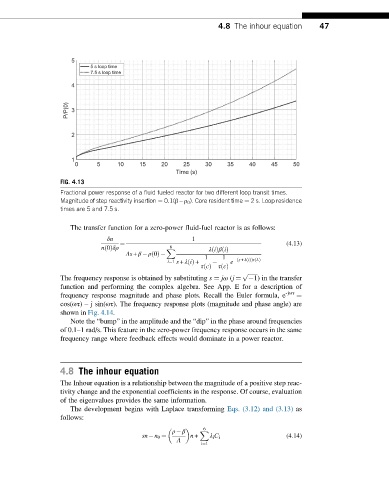
FIG. 4.13
Fractional power response of a fluid fueled reactor for two different loop transit times.
Magnitude of step reactivity insertion ¼ 0.1(β – ρ 0 ). Core resident time ¼ 2 s. Loop residence
times are 5 and 7.5 s.

The transfer function for a zero-power fluid-fuel reactor is as follows:
δn 1
n 0ðÞδρ ¼ X λ iðÞβ iðÞ (4.13)
6
Λs + β ρ 0ðÞ
1 1
ð
i¼1 s + λ iðÞ + e s + λ iðÞÞτ LðÞ
τ cðÞ τ cðÞ
p ffiffiffiffiffiffiffi
The frequency response is obtained by substituting s ¼ jω (j ¼ 1) in the transfer
function and performing the complex algebra. See App. E for a description of
frequency response magnitude and phase plots. Recall the Euler formula, e -jωτ ¼
cos(ωτ) – jsin(ωτ). The frequency response plots (magnitude and phase angle) are
shown in Fig. 4.14.
Note the “bump” in the amplitude and the “dip” in the phase around frequencies
of 0.1–1 rad/s. This feature in the zero-power frequency response occurs in the same
frequency range where feedback effects would dominate in a power reactor.

4.8 The inhour equation
The Inhour equation is a relationship between the magnitude of a positive step reac-
tivity change and the exponential coefficients in the response. Of course, evaluation
of the eigenvalues provides the same information.
The development begins with Laplace transforming Eqs. (3.12) and (3.13) as
follows:
ρ β X
6
sn n 0 ¼ n + λ i C i (4.14)
Λ
i¼1