Page 328 - Dynamics of Mechanical Systems

0593_C09_fm Page 309 Monday, May 6, 2002 2:50 PM

Principles of Impulse and Momentum 309

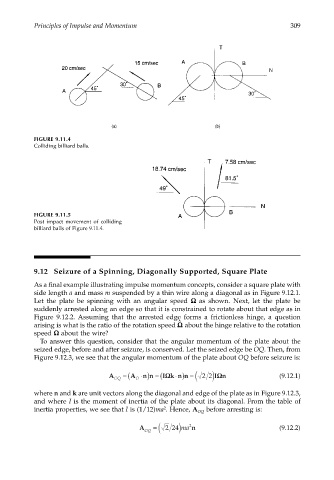
FIGURE 9.11.4
Colliding billiard balls.

FIGURE 9.11.5
Post impact movement of colliding
billiard balls of Figure 9.11.4.

9.12 Seizure of a Spinning, Diagonally Supported, Square Plate
As a final example illustrating impulse momentum concepts, consider a square plate with
side length a and mass m suspended by a thin wire along a diagonal as in Figure 9.12.1.
Let the plate be spinning with an angular speed ΩΩ ΩΩ as shown. Next, let the plate be
suddenly arrested along an edge so that it is constrained to rotate about that edge as in
Figure 9.12.2. Assuming that the arrested edge forms a frictionless hinge, a question
ˆ
arising is what is the ratio of the rotation speed ΩΩ ΩΩ about the hinge relative to the rotation
speed ΩΩ ΩΩ about the wire?
To answer this question, consider that the angular momentum of the plate about the
seized edge, before and after seizure, is conserved. Let the seized edge be OQ. Then, from
Figure 9.12.3, we see that the angular momentum of the plate about OQ before seizure is:
OQ ( A ⋅ ) = ( ΩΩ ⋅ ) Ω
=
Ω
A O nn I k nn ) = ( 22 I n (9.12.1)
where n and k are unit vectors along the diagonal and edge of the plate as in Figure 9.12.3,
and where I is the moment of inertia of the plate about its diagonal. From the table of
2
inertia properties, we see that I is (1/12)ma . Hence, A before arresting is:
OQ
=
A OQ ( 224 ma ) 2 n (9.12.2)