Page 32 - Electrical Properties of Materials

Waves in the presence of an applied magnetic field: cyclotron resonance 15

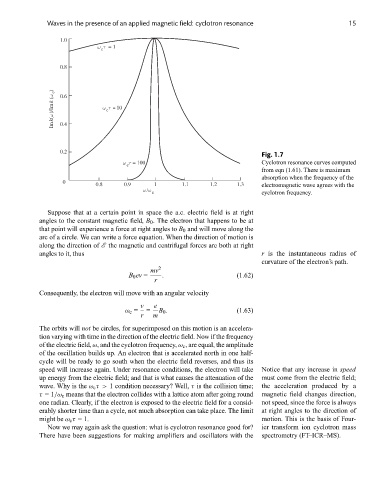
1.0
ω τ = 1
c

0.8

Imk(ω )/Im k (ω c ) 0.6 ω τ = 10

c
0.4

0.2
Fig. 1.7
ω τ = 100 Cyclotron resonance curves computed
c
from eqn (1.61). There is maximum
absorption when the frequency of the
0 0.8 0.9 1 1.1 1.2 1.3 electromagnetic wave agrees with the
ω /ω
c cyclotron frequency.

Suppose that at a certain point in space the a.c. electric field is at right
angles to the constant magnetic field, B 0 . The electron that happens to be at
that point will experience a force at right angles to B 0 and will move along the
arc of a circle. We can write a force equation. When the direction of motion is
along the direction of E the magnetic and centrifugal forces are both at right
angles to it, thus r is the instantaneous radius of
curvature of the electron’s path.
mv 2
B 0 ev = . (1.62)
r

Consequently, the electron will move with an angular velocity
v e
ω c = = B 0 . (1.63)
r m
The orbits will not be circles, for superimposed on this motion is an accelera-
tion varying with time in the direction of the electric field. Now if the frequency
of the electric field, ω, and the cyclotron frequency, ω c , are equal, the amplitude
of the oscillation builds up. An electron that is accelerated north in one half-
cycle will be ready to go south when the electric field reverses, and thus its
speed will increase again. Under resonance conditions, the electron will take Notice that any increase in speed
up energy from the electric field; and that is what causes the attenuation of the must come from the electric field;
wave. Why is the ω c τ> 1 condition necessary? Well, τ is the collision time; the acceleration produced by a
τ =1/ω c means that the electron collides with a lattice atom after going round magnetic field changes direction,
one radian. Clearly, if the electron is exposed to the electric field for a consid- not speed, since the force is always
erably shorter time than a cycle, not much absorption can take place. The limit at right angles to the direction of
might be ω c τ =1. motion. This is the basis of Four-
Now we may again ask the question: what is cyclotron resonance good for? ier transform ion cyclotron mass
There have been suggestions for making amplifiers and oscillators with the spectrometry (FT–ICR–MS).