Page 343 - Electrical Properties of Materials

Masers 325

The material used is ruby, which happens to be good both for lasers and
masers. For trebly ionized chromium, the outer 3d-shell has three electrons of
identical spin. Hence its total spin contribution is 3/2. The contribution from
orbital angular momentum is taken as zero, thus j =3/2, leading to the values ∗ There is some theoretical justification
∗
for doing so, but the real reason is that
3 1 1 3 unless orbital momentum is disregarded,
M J = , ,– ,– . (12.53) there is no resemblance at all between
2 2 2 2
theory and experiment.
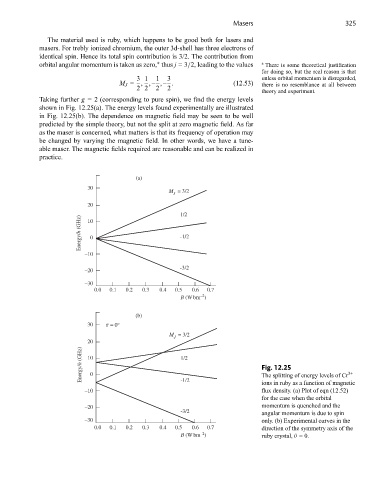
Taking further g = 2 (corresponding to pure spin), we find the energy levels
shown in Fig. 12.25(a). The energy levels found experimentally are illustrated
in Fig. 12.25(b). The dependence on magnetic field may be seen to be well
predicted by the simple theory, but not the split at zero magnetic field. As far
as the maser is concerned, what matters is that its frequency of operation may
be changed by varying the magnetic field. In other words, we have a tune-
able maser. The magnetic fields required are reasonable and can be realized in
practice.

(a)
30
M = 3/2
J
20
1/2
Energy/h (GHz) 0 -1/2
10

–10
-3/2
–20
–30
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
–2
B (Wbm )

(b)
30 θ = 0°
M = 3/2
J
20
Energy/h (GHz) 10 0 1/2 Fig. 12.25 3+

The splitting of energy levels of Cr
flux density. (a) Plot of eqn (12.52)
–10 -1/2 ions in ruby as a function of magnetic
for the case when the orbital
–20 momentum is quenched and the
-3/2 angular momentum is due to spin
–30 only. (b) Experimental curves in the
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 direction of the symmetry axis of the
–2
B (Wbm ) ruby crystal, θ =0.