Page 74 - Electrical Properties of Materials

The hydrogen atom 57

2 2
|ψ| r

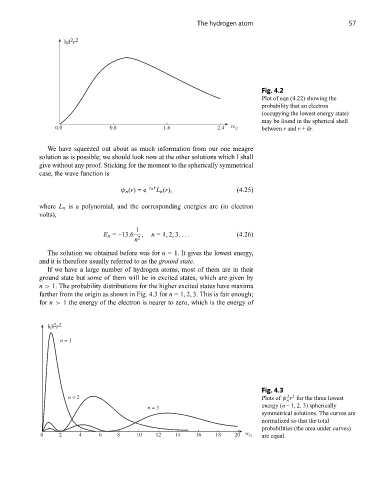
Fig. 4.2
Plot of eqn (4.22) showing the
probability that an electron
(occupying the lowest energy state)
may be found in the spherical shell
0 . 0 0.8 6 . 1 4 . 2 rc 0 between r and r +dr.

We have squeezed out about as much information from our one meagre
solution as is possible; we should look now at the other solutions which I shall
give without any proof. Sticking for the moment to the spherically symmetrical
case, the wave function is

ψ n (r)=e –c n r L n (r), (4.25)

where L n is a polynomial, and the corresponding energies are (in electron
volts),

1
E n = –13.6 , n = 1,2,3. ... (4.26)
n 2
The solution we obtained before was for n = 1. It gives the lowest energy,
and it is therefore usually referred to as the ground state.
If we have a large number of hydrogen atoms, most of them are in their
ground state but some of them will be in excited states, which are given by
n > 1. The probability distributions for the higher excited states have maxima
farther from the origin as shown in Fig. 4.3 for n = 1, 2, 3. This is fair enough;
for n > 1 the energy of the electron is nearer to zero, which is the energy of

2 2
|ψ| r
n = 1

Fig. 4.3
2 2
n = 2 Plots of ψ r for the three lowest
n
n = 3 energy (n = 1, 2, 3) spherically
symmetrical solutions. The curves are
normalized so that the total
probabilities (the area under curves)
0 2 4 6 8 10 12 14 16 18 20 rc 0 are equal.