Page 113 - Electromagnetics

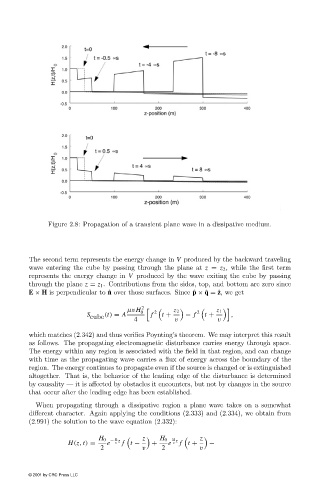
Figure 2.8: Propagation of a transient plane wave in a dissipative medium.

The second term represents the energy change in V produced by the backward traveling
wave entering the cube by passing through the plane at z = z 2 , while the first term
represents the energy change in V produced by the wave exiting the cube by passing
through the plane z = z 1 . Contributions from the sides, top, and bottom are zero since
E × H is perpendicular to ˆ n over those surfaces. Since ˆ p × ˆ q = ˆ z,weget

µvH 0 2 2 z 2 2 z 1
S cube (t) = A f t + − f t + ,
4 v v
which matches (2.342) and thus verifies Poynting’s theorem. We may interpret this result
as follows. The propagating electromagnetic disturbance carries energy through space.
The energy within any region is associated with the field in that region, and can change
with time as the propagating wave carries a flux of energy across the boundary of the
region. The energy continues to propagate even if the source is changed or is extinguished
altogether. That is, the behavior of the leading edge of the disturbance is determined
by causality — it is affected by obstacles it encounters, but not by changes in the source
that occur after the leading edge has been established.
When propagating through a dissipative region a plane wave takes on a somewhat
different character. Again applying the conditions (2.333) and (2.334), we obtain from
(2.991) the solution to the wave equation (2.332):

H 0 − z z H 0 z z
H(z, t) = e v f t − + e v f t + −
2 v 2 v

© 2001 by CRC Press LLC