Page 110 - Electromagnetics
P. 110
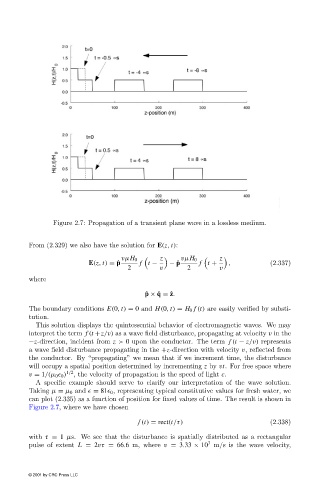
Figure 2.7: Propagation of a transient plane wave in a lossless medium.
From (2.329) we also have the solution for E(z, t):
vµH 0 z vµH 0 z
E(z, t) = ˆ p f t − − ˆ p f t + , (2.337)
2 v 2 v
where
ˆ p × ˆ q = ˆ z.
The boundary conditions E(0, t) = 0 and H(0, t) = H 0 f (t) are easily verified by substi-
tution.
This solution displays the quintessential behavior of electromagnetic waves. We may
interpret the term f (t +z/v) as a wave field disturbance, propagating at velocity v in the
−z-direction, incident from z > 0 upon the conductor. The term f (t − z/v) represents
a wave field disturbance propagating in the +z-direction with velocity v, reflected from
the conductor. By “propagating” we mean that if we increment time, the disturbance
will occupy a spatial position determined by incrementing z by vt. For free space where
v = 1/(µ 0
0 ) 1/2 , the velocity of propagation is the speed of light c.
A specific example should serve to clarify our interpretation of the wave solution.
Taking µ = µ 0 and
= 81
0 , representing typical constitutive values for fresh water, we
can plot (2.335) as a function of position for fixed values of time. The result is shown in
Figure 2.7, where we have chosen
f (t) = rect(t/τ) (2.338)
with τ = 1 µs. We see that the disturbance is spatially distributed as a rectangular
7
pulse of extent L = 2vτ = 66.6 m, where v = 3.33 × 10 m/s is the wave velocity,
© 2001 by CRC Press LLC