Page 182 - Electromagnetics

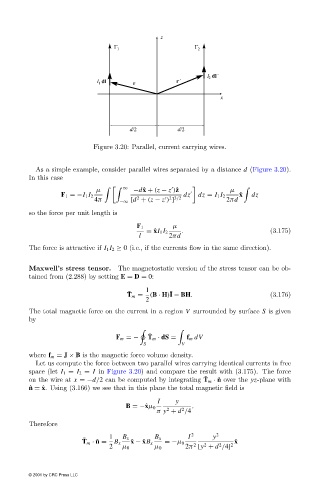
Figure 3.20: Parallel, current carrying wires.

As a simple example, consider parallel wires separated by a distance d (Figure 3.20).
In this case
µ ∞ −d ˆ x + (z − z )ˆ z µ

F 1 =−I 1 I 2 2 2 3/2 dz dz = I 1 I 2 ˆ x dz
4π −∞ [d + (z − z ) ] 2πd
so the force per unit length is
µ
F 1
= ˆ xI 1 I 2 . (3.175)
l 2πd
The force is attractive if I 1 I 2 ≥ 0 (i.e., if the currents flow in the same direction).

Maxwell’s stress tensor. The magnetostatic version of the stress tensor can be ob-
tained from (2.288)by setting E = D = 0:
1
¯ ¯
T m = (B · H)I − BH. (3.176)
2
The total magnetic force on the current in a region V surrounded by surface S is given
by

¯
F m =− T m · dS = f m dV
S V
where f m = J × B is the magnetic force volume density.
Let us compute the force between two parallel wires carrying identical currents in free
space (let I 1 = I 2 = I in Figure 3.20)and compare the result with (3.175). The force
¯
on the wire at x =−d/2 can be computed by integrating T m · ˆ n over the yz-plane with
ˆ n = ˆ x. Using (3.166)we see that in this plane the total magnetic field is
I y
B =−ˆ xµ 0 2 2 .
π y + d /4
Therefore

1 B x B x I 2 y 2
¯
T m · ˆ n = B x ˆ x − ˆ xB x =−µ 0 ˆ x
2
2
2
2 µ 0 µ 0 2π [y + d /4] 2
© 2001 by CRC Press LLC