Page 111 -

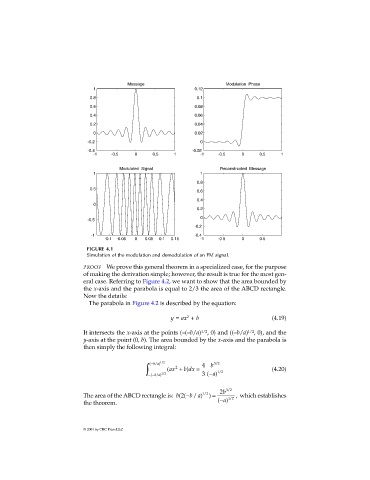
FIGURE 4.1
Simulation of the modulation and demodulation of an FM signal.
PROOF We prove this general theorem in a specialized case, for the purpose
of making the derivation simple; however, the result is true for the most gen-
eral case. Referring to Figure 4.2, we want to show that the area bounded by
the x-axis and the parabola is equal to 2/3 the area of the ABCD rectangle.
Now the details:
The parabola in Figure 4.2 is described by the equation:

2
y = ax + b (4.19)
It intersects the x-axis at the points (–(–b/a) 1/2 , 0) and ((–b/a) 1/2 , 0), and the
y-axis at the point (0, b). The area bounded by the x-axis and the parabola is
then simply the following integral:

( ba−
/
/
∫ −− / ) 12 / (ax + ) b dx = 4 ( a− b 32 / 12 (4.20)
2
)
3
12
( ba
/ )
/
The area of the ABCD rectangle is: b((2 − b a/ ) 12 ) = b 2 32 / 12 , which establishes
/
the theorem. (− a)
© 2001 by CRC Press LLC