Page 145 -

x0(k)=fzero('besselj(0,x)',(pi/4)*p(k));
x0approx(k)=(pi/4)*p(k)+(1/(2*pi))*(p(k)^(-1))-...
(31/6)*(1/pi^3)*(p(k)^(-3))+...
(3779/15)*(1/pi^5)*(p(k)^(-5));
end
kk=1:10;
subplot(2,1,1);
plot(kk,x0,'o')
title('Zeros of Zero Order BesselJ Function')
subplot(2,1,2);
semilogy(kk,x0-x0approx,'o')
title('Error in Approximate Values of the Zeros')
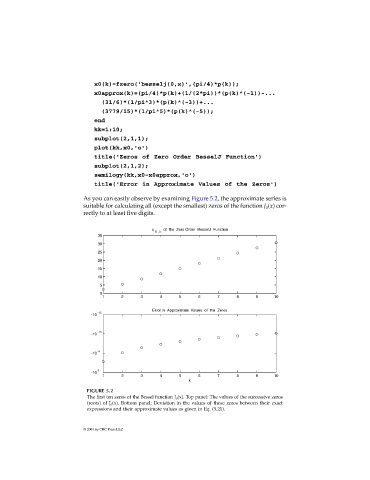
As you can easily observe by examining Figure 5.2, the approximate series is
suitable for calculating all (except the smallest) zeros of the function J (x) cor-
0
rectly to at least five digits.

FIGURE 5.2
The first ten zeros of the Bessel function J 0 (x). Top panel: The values of the successive zeros
(roots) of J 0 (x). Bottom panel: Deviation in the values of these zeros between their exact
expressions and their approximate values as given in Eq. (5.21).

© 2001 by CRC Press LLC