Page 233 -

Solution: The conditions for the above theorem are satisfied, and

 1
c =  l + ∫ 1 P x dx() (7.113)
l  2 a l

From Eq. (7.96), and noting that P (1) = 1, we find that:
l

c = 1 ( 1− a) (7.114)
0
2
and

1
c =− [ P ( a −) P ( a)] (7.115)
l l+1 l−1
2
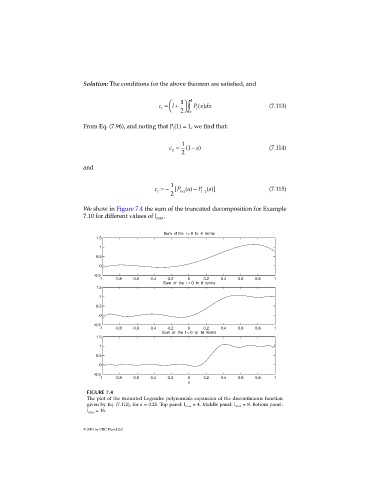
We show in Figure 7.4 the sum of the truncated decomposition for Example
7.10 for different values of l max .

FIGURE 7.4
The plot of the truncated Legendre polynomials expansion of the discontinuous function
given by Eq. (7.112), for a = 0.25. Top panel: l max = 4. Middle panel: l max = 8. Bottom panel:
l max = 16.

© 2001 by CRC Press LLC