Page 53 -

30 1. Elementary Properties of the Chord-Tangent Group Law on a Cubic Curve

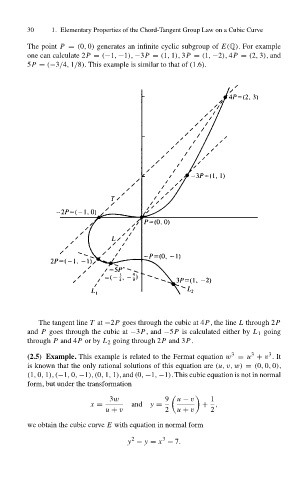
The point P = (0, 0) generates an infinite cyclic subgroup of E(Q). For example
one can calculate 2P = (−1, −1), −3P = (1, 1),3P = (1, −2),4P = (2, 3),and
5P = (−3/4, 1/8). This example is similar to that of (1.6).

The tangent line T at −2P goes through the cubic at 4P, the line L through 2P
and P goes through the cubic at −3P,and −5P is calculated either by L 1 going
through P and 4P or by L 2 going through 2P and 3P.
3
3
3
(2.5) Example. This example is related to the Fermat equation w = u + v .It
is known that the only rational solutions of this equation are (u,v,w) = (0, 0, 0),
(1, 0, 1), (−1, 0, −1), (0, 1, 1),and (0, −1, −1). This cubic equation is not in normal
form, but under the transformation

3w 9 u − v 1
x = and y = + ,
u + v 2 u + v 2
we obtain the cubic curve E with equation in normal form
2 3
y − y = x − 7.