Page 217 - Academic Press Encyclopedia of Physical Science and Technology 3rd BioTechnology

P1: ZBU Final Pages
Encyclopedia of Physical Science and Technology EN011J-141 July 31, 2001 15:14

794 Pharmaceuticals, Controlled Release of

AP c
dM t
= , (1)
dt l
where dM t /dt is the device release rate, A is the total
area of the laminate, P is the membrane permeability, l is
the membrane thickness, and c is the difference in drug
concentration between the solution at the inside surface of
the membrane and the drug concentration in the solution at
the outer surface of the membrane, usually close to zero.
When the solution inside the enclosure is saturated, the
drug concentration is c s , and Eq. (1) reduces to
dM t APc s
= . (2)
dt l
Drug release is then constant as long as a saturated solu-
tion is maintained within the enclosure. The total duration
of constant release depends on the initial volume of the
enclosure V , the mass of encapsulated drug M 0 , and the
solubility of the drug c s . The mass of agent that can be
delivered at a constant rate is M 0 − c s V . Thus, it follows
that the duration of constant release t ∞ is
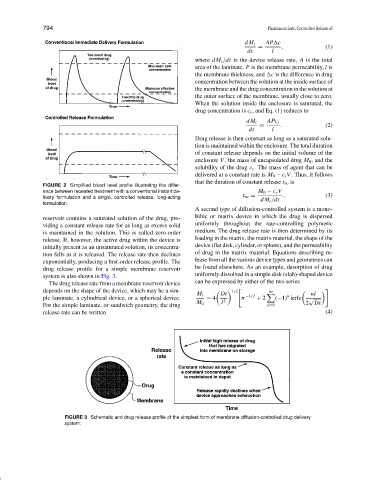
FIGURE 2 Simplified blood level profile illustrating the differ-
ence between repeated treatment with a conventional instant de- M 0 − c s V
livery formulation and a single, controlled release, long-acting t ∞ = dM t /dt . (3)
formulation.
A second type of diffusion-controlled system is a mono-
reservoir contains a saturated solution of the drug, pro- lithic or matrix device in which the drug is dispersed
viding a constant release rate for as long as excess solid uniformly throughout the rate-controlling polymeric
is maintained in the solution. This is called zero-order medium. The drug release rate is then determined by its
release. If, however, the active drug within the device is loading in the matrix, the matrix material, the shape of the
initially present as an unsaturated solution, its concentra- device (flat disk, cylinder, or sphere), and the permeability
tion falls as it is released. The release rate then declines of drug in the matrix material. Equations describing re-
exponentially, producing a first-order release profile. The lease from all the various device types and geometries can
drug release profile for a simple membrane reservoir be found elsewhere. As an example, desorption of drug
system is also shown in Fig. 3. uniformly dissolved in a simple disk (slab)-shaped device
The drug release rate from a membrane reservoir device can be expressed by either of the two series
depends on the shape of the device, which may be a sim- 1/2 ∞
M t Dt −1/2 n nl
ple laminate, a cylindrical device, or a spherical device. = 4 2 π + 2 (−1) ierfc √
For the simple laminate, or sandwich geometry, the drug M 0 l n=0 2 Dt
release rate can be written (4)

FIGURE 3 Schematic and drug release profile of the simplest form of membrane diffusion-controlled drug delivery
system.