Page 64 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: FWD Revised Pages
Encyclopedia of Physical Science and Technology En001c-14 May 7, 2001 18:25

Aerosols 287

analogous to a molecular diffusivity. Using the theory of
Brownian motion, Einstein derived the relationship for
particle diffusivity:

D p = kT/ m p = BkT
Here, k is Boltzmann’s constant and m p particle mass. In
analogy to a simple kinetic theory of gases, the defini-
−1
tion of a mean free path for particles is λ p = ¯υ p . The
average thermal speed of particle is
1/2
8kT π

¯ υ p = and D p = ¯ υ p λ p
πm p 8
Some characteristic values of these aerosol transport prop-
erties of particles in air are listed in Table II and Fig. 1.

7. Diffusion in Flowing Media
When aerosols are in a flow configuration, diffusion by
Brownian motion can take place, causing deposition to
surfaces, independent of inertial forces. The rate of depo-
sition depends on the flow rate, the particle diffusivity, the
gradient in particle concentration, and the geometry of the
collecting obstacle. The diffusion processes are the key to
the effectiveness of gas filters, as we shall see later.
A particle agitation analogous to Brownian motion is
induced by turbulence in an aerosol. Turbulence is a form
of eddying fluid motion often observed in atomospheric
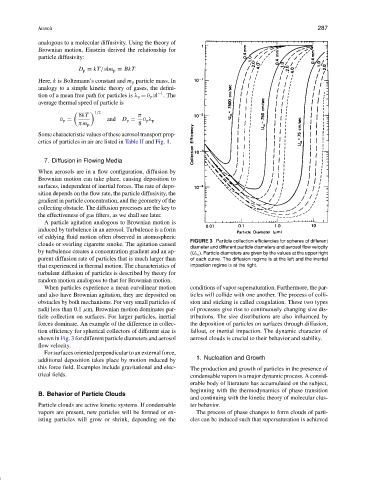
FIGURE 3 Particle collection efficiencies for spheres of different
clouds or swirling cigarette smoke. The agitation caused
diameter and different particle diameters and aerosol flow velocity
by turbulence creates a concentration gradient and an ap- (U ∞ ). Particle diameters are given by the values at the upper right
parent diffusion rate of particles that is much larger than of each curve. The diffusion regime is at the left and the inertial
that experienced in thermal motion. The characteristics of impaction regime is at the right.
turbulent diffusion of particles is described by theory for
random motion analogous to that for Brownian motion.
When particles experience a mean curvilinear motion conditions of vapor supersaturation. Furthermore, the par-
and also have Brownian agitation, they are deposited on ticles will collide with one another. The process of colli-
obstacles by both mechanisms. For very small particles of sion and sticking is called coagulation. These two types
radii less than 0.1 µm, Brownian motion dominates par- of processes give rise to continuously changing size dis-
ticle collection on surfaces. For larger particles, inertial tributions. The size distributions are also influenced by
forces dominate. An example of the difference in collec- the deposition of particles on surfaces through diffusion,
tion efficiency for spherical collectors of different size is fallout, or inertial impaction. The dynamic character of
shown in Fig. 3 for different particle diameters and aerosol aerosol clouds is crucial to their behavior and stability.
flow velocity.
For surfaces oriented perpendicular to an external force,
additional deposition takes place by motion induced by 1. Nucleation and Growth
this force field. Examples include gravitational and elec- The production and growth of particles in the presence of
trical fields. condensable vapors is a major dynamic process. A consid-
erable body of literature has accumulated on the subject,
beginning with the thermodynamics of phase transition
B. Behavior of Particle Clouds
and continuing with the kinetic theory of molecular clus-
Particle clouds are active kinetic systems. If condensable ter behavior.
vapors are present, new particles will be formed or ex- The process of phase changes to form clouds of parti-
isting particles will grow or shrink, depending on the cles can be induced such that supersaturation is achieved