Page 277 - Engineering Electromagnetics, 8th Edition

CHAPTER 8 Magnetic Forces, Materials, and Inductance 259

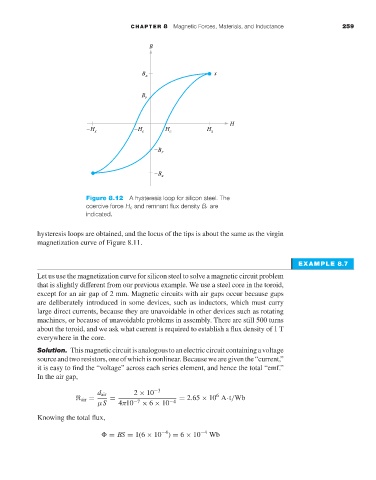
Figure 8.12 A hysteresis loop for silicon steel. The
coercive force H c and remnant flux density B r are
indicated.

hysteresis loops are obtained, and the locus of the tips is about the same as the virgin
magnetization curve of Figure 8.11.

EXAMPLE 8.7
Let us use the magnetization curve for silicon steel to solve a magnetic circuit problem
that is slightly different from our previous example. We use a steel core in the toroid,
except for an air gap of 2 mm. Magnetic circuits with air gaps occur because gaps
are deliberately introduced in some devices, such as inductors, which must carry
large direct currents, because they are unavoidable in other devices such as rotating
machines, or because of unavoidable problems in assembly. There are still 500 turns
about the toroid, and we ask what current is required to establish a flux density of 1 T
everywhere in the core.
Solution. Thismagneticcircuitisanalogoustoanelectriccircuitcontainingavoltage
sourceandtworesistors,oneofwhichisnonlinear.Becausewearegiventhe“current,”
it is easy to find the “voltage” across each series element, and hence the total “emf.”
In the air gap,

d air 2 × 10 −3 6
air = = = 2.65 × 10 A·t/Wb
µS 4π10 −7 × 6 × 10 −4
Knowing the total flux,
−4
= BS = 1(6 × 10 ) = 6 × 10 −4 Wb