Page 316 - Engineering Electromagnetics, 8th Edition

298 ENGINEERING ELECTROMAGNETICS

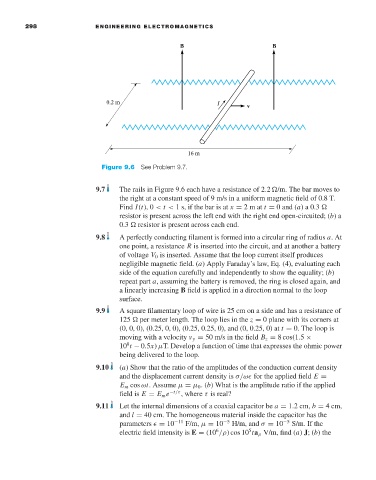
Figure 9.6 See Problem 9.7.

9.7 The rails in Figure 9.6 each have a resistance of 2.2 /m. The bar moves to
the right at a constant speed of 9 m/s in a uniform magnetic field of 0.8 T.
Find I(t), 0 < t < 1s,ifthe bar is at x = 2mat t = 0 and (a)a 0.3
resistor is present across the left end with the right end open-circuited; (b)a
0.3 resistor is present across each end.
9.8 A perfectly conducting filament is formed into a circular ring of radius a.At
one point, a resistance R is inserted into the circuit, and at another a battery
of voltage V 0 is inserted. Assume that the loop current itself produces
negligible magnetic field. (a) Apply Faraday’s law, Eq. (4), evaluating each
side of the equation carefully and independently to show the equality; (b)
repeat part a, assuming the battery is removed, the ring is closed again, and
a linearly increasing B field is applied in a direction normal to the loop
surface.
9.9 A square filamentary loop of wire is 25 cm on a side and has a resistance of
125 per meter length. The loop lies in the z = 0 plane with its corners at
(0, 0, 0), (0.25, 0, 0), (0.25, 0.25, 0), and (0, 0.25, 0) at t = 0. The loop is
moving with a velocity v y = 50 m/s in the field B z = 8 cos(1.5 ×
8
10 t − 0.5x) µT. Develop a function of time that expresses the ohmic power
being delivered to the loop.
9.10 (a) Show that the ratio of the amplitudes of the conduction current density
and the displacement current density is σ/ω for the applied field E =
E m cos ωt. Assume µ = µ 0 .(b) What is the amplitude ratio if the applied
field is E = E m e −t/τ , where τ is real?
9.11 Let the internal dimensions of a coaxial capacitor be a = 1.2 cm, b = 4 cm,
and l = 40 cm. The homogeneous material inside the capacitor has the
parameters = 10 −11 F/m, µ = 10 −5 H/m, and σ = 10 −5 S/m. If the
5
6
electric field intensity is E = (10 /ρ) cos 10 ta ρ V/m, find (a) J;(b) the