Page 589 - Engineering Electromagnetics, 8th Edition

APPENDIX E Origins of the Complex Permittivity 571

res

res

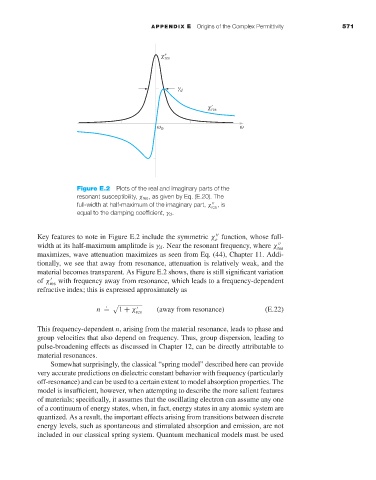
Figure E.2 Plots of the real and imaginary parts of the
resonant susceptibility, χ res ,as given by Eq. (E.20). The
full-width at half-maximum of the imaginary part, χ ,is

res
equal to the damping coefficient, γ d .
Key features to note in Figure E.2 include the symmetric χ function, whose full-

e

width at its half-maximum amplitude is γ d . Near the resonant frequency, where χ res
maximizes, wave attenuation maximizes as seen from Eq. (44), Chapter 11. Addi-
tionally, we see that away from resonance, attenuation is relatively weak, and the
material becomes transparent. As Figure E.2 shows, there is still significant variation

of χ res with frequency away from resonance, which leads to a frequency-dependent
refractive index; this is expressed approximately as
.

n = 1 + χ res (away from resonance) (E.22)
This frequency-dependent n, arising from the material resonance, leads to phase and
group velocities that also depend on frequency. Thus, group dispersion, leading to
pulse-broadening effects as discussed in Chapter 12, can be directly attributable to
material resonances.
Somewhat surprisingly, the classical “spring model” described here can provide
very accurate predictions on dielectric constant behavior with frequency (particularly
off-resonance) and can be used to a certain extent to model absorption properties. The
model is insufficient, however, when attempting to describe the more salient features
of materials; specifically, it assumes that the oscillating electron can assume any one
of a continuum of energy states, when, in fact, energy states in any atomic system are
quantized. As a result, the important effects arising from transitions between discrete
energy levels, such as spontaneous and stimulated absorption and emission, are not
included in our classical spring system. Quantum mechanical models must be used