Page 96 - Engineering Electromagnetics, 8th Edition

78 ENGINEERING ELECTROMAGNETICS

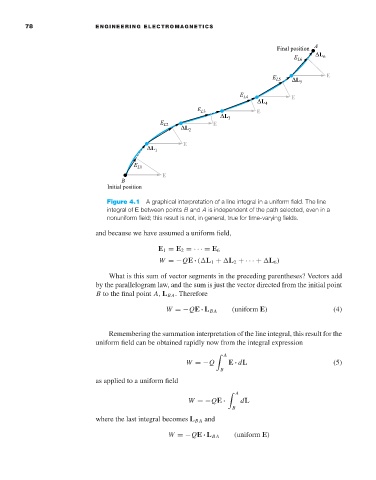
Figure 4.1 A graphical interpretation of a line integral in a uniform field. The line
integral of E between points B and A is independent of the path selected, even in a
nonuniform field; this result is not, in general, true for time-varying fields.
and because we have assumed a uniform field,

E 1 = E 2 = ··· = E 6
W =−QE · ( L 1 + L 2 +· · ·+ L 6 )

What is this sum of vector segments in the preceding parentheses? Vectors add
by the parallelogram law, and the sum is just the vector directed from the initial point
B to the final point A, L BA . Therefore

W =−QE · L BA (uniform E) (4)

Remembering the summation interpretation of the line integral, this result for the
uniform field can be obtained rapidly now from the integral expression

A
W =−Q E · dL (5)
B
as applied to a uniform field
A
W =−QE · dL
B
where the last integral becomes L BA and

W =−QE · L BA (uniform E)