Page 70 - Essentials of applied mathematics for scientists and engineers

book Mobk070 March 22, 2007 11:7

60 ESSENTIALS OF APPLIED MATHEMATICS FOR SCIENTISTS AND ENGINEERS

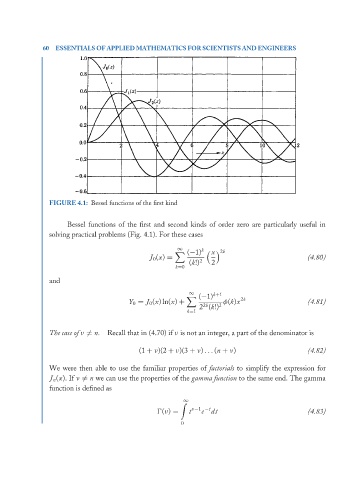
FIGURE 4.1: Bessel functions of the first kind

Bessel functions of the first and second kinds of order zero are particularly useful in
solving practical problems (Fig. 4.1). For these cases

∞
x
(−1) k 2k

J 0 (x) = (4.80)
(k!) 2 2
k=0
and
∞ k+1
(−1)
2k
Y 0 = J 0 (x)ln(x) + φ(k)x (4.81)
2k
2 (k!) 2
k=1
The case of ν = n. Recall that in (4.70) if ν is not an integer, a part of the denominator is

(1 + ν)(2 + ν)(3 + ν) ... (n + ν) (4.82)

We were then able to use the familiar properties of factorials to simplify the expression for
J n (x). If ν = n we can use the properties of the gamma function to the same end. The gamma
function is defined as
∞

e dt
(ν) = t ν−1 −t (4.83)
0