Page 133 - Essentials of physical chemistry

The Second and Third Laws of Thermodynamics 95

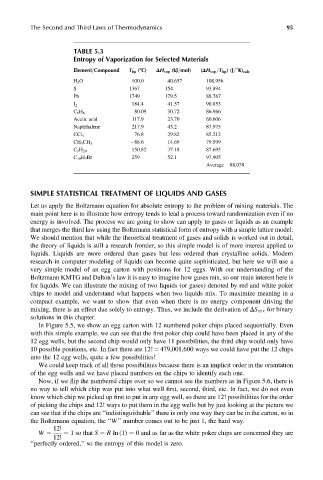
TABLE 5.3
Entropy of Vaporization for Selected Materials
Element=Compound T bp (8C) DH vap (kJ=mol) (DH vap =T bp )(J= K) calc

H 2 O 100.0 40.657 108.956
S 1367 154 93.894
Pb 1749 179.5 88.767
I 2 184.4 41.57 90.853
80.09 30.72 86.966
C 6 H 6
Acetic acid 117.9 23.70 60.606
Naphthalene 217.9 43.2 87.975
76.8 29.82 85.212
CCl 4
88.6 14.69 79.599
CH 3 CH 3
150.82 37.18 87.695
C 9 H 20
C 10 H 7 Br 259 52.1 97.905
Average ¼ 88.039

SIMPLE STATISTICAL TREATMENT OF LIQUIDS AND GASES
Let us apply the Boltzmann equation for absolute entropy to the problem of mixing materials. The
main point here is to illustrate how entropy tends to lead a process toward randomization even if no
energy is involved. The process we are going to show can apply to gases or liquids as an example
that merges the third law using the Boltzmann statistical form of entropy with a simple lattice model.
We should mention that while the theoretical treatment of gases and solids is worked out in detail,
the theory of liquids is still a research frontier, so this simple model is of more interest applied to
liquids. Liquids are more ordered than gases but less ordered than crystalline solids. Modern
research in computer modeling of liquids can become quite sophisticated, but here we will use a
very simple model of an egg carton with positions for 12 eggs. With our understanding of the
Boltzmann KMTG and Dalton’s law it is easy to imagine how gases mix, so our main interest here is
for liquids. We can illustrate the mixing of two liquids (or gases) denoted by red and white poker
chips to model and understand what happens when two liquids mix. To maximize meaning in a
compact example, we want to show that even when there is no energy component driving the
mixing, there is an effect due solely to entropy. Thus, we include the derivation of DS mix for binary
solutions in this chapter.
In Figure 5.5, we show an egg carton with 12 numbered poker chips placed sequentially. Even
with this simple example, we can see that the first poker chip could have been placed in any of the
12 egg wells, but the second chip would only have 11 possibilities, the third chip would only have
10 possible positions, etc. In fact there are 12! ¼ 479,001,600 ways we could have put the 12 chips
into the 12 egg wells, quite a few possibilities!
We could keep track of all those possibilities because there is an implicit order in the orientation
of the egg wells and we have placed numbers on the chips to identify each one.
Now, if we flip the numbered chips over so we cannot see the numbers as in Figure 5.6, there is
no way to tell which chip was put into what well first, second, third, etc. In fact, we do not even
know which chip we picked up first to put in any egg well, so there are 12! possibilities for the order
of picking the chips and 12! ways to put them in the egg wells but by just looking at the picture we
can see that if the chips are ‘‘indistinguishable’’ there is only one way they can be in the carton, so in
the Boltzmann equation, the ‘‘W’’ number comes out to be just 1, the hard way.
12!
¼ 1 so that S ¼ R ln (1) ¼ 0 and as far as the white poker chips are concerned they are
12!
W ¼
‘‘perfectly ordered,’’ so the entropy of this model is zero.