Page 137 - Essentials of physical chemistry

The Second and Third Laws of Thermodynamics 99

1000

500
G(J)=–S*298.15; S*100(J/°) –500 0 0 0.2 0.4 0.6 0.8 1 1.2

–1000

–1500

–2000
X mole fraction
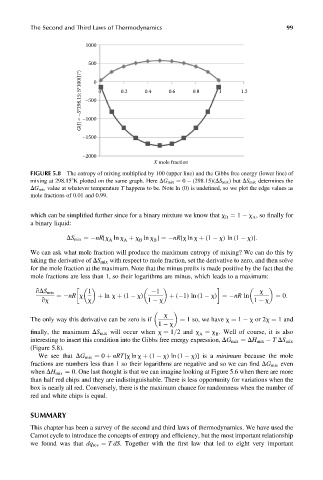
FIGURE 5.8 The entropy of mixing multiplied by 100 (upper line) and the Gibbs free energy (lower line) of
mixing at 298.158K plotted on the same graph. Here DG mix ¼ 0 (298:15)(DS mix ) but DS mix determines the
DG mix value at whatever temperature T happens to be. Note ln (0) is undefined, so we plot the edge values as
mole fractions of 0.01 and 0.99.

which can be simplified further since for a binary mixture we know that x ¼ 1 x ,so finally for
B A
a binary liquid:
DS mix ¼ nR[x ln x þ x ln x ] ¼ nR[x ln x þ (1 x)ln (1 x)]:
A A B B
We can ask what mole fraction will produce the maximum entropy of mixing? We can do this by
taking the derivative of DS mix with respect to mole fraction, set the derivative to zero, and then solve
for the mole fraction at the maximum. Note that the minus prefix is made positive by the fact that the
mole fractions are less than 1, so their logarithms are minus, which leads to a maximum:

qDS mix 1 1 x
¼ nR x þ ln x þ (1 x) þ ( 1)ln (1 x) ¼ nR ln ¼ 0:
qx x 1 x 1 x

x
The only way this derivative can be zero is if ¼ 1 so, we have x ¼ 1 x or 2x ¼ 1 and
1 x
finally, the maximum DS mix will occur when x ¼ 1=2 and x ¼ x . Well of course, it is also
A B
interesting to insert this condition into the Gibbs free energy expression, DG mix ¼ DH mix T DS mix
(Figure 5.8).
We see that DG mix ¼ 0 þ nRT[x ln x þ (1 x)ln (1 x)] is a minimum because the mole
fractions are numbers less than 1 so their logarithms are negative and so we can find DG mix even
when DH mix ¼ 0. One last thought is that we can imagine looking at Figure 5.6 when there are more
than half red chips and they are indistinguishable. There is less opportunity for variations when the
box is nearly all red. Conversely, there is the maximum chance for randomness when the number of
red and white chips is equal.

SUMMARY
This chapter has been a survey of the second and third laws of thermodynamics. We have used the
Carnot cycle to introduce the concepts of entropy and efficiency, but the most important relationship
we found was that dq rev ¼ TdS. Together with the first law that led to eight very important