Page 178 - Excel for Scientists and Engineers: Numerical Methods

CHAPTER 8 ROOTS OF EOUATIONS 155

1 2 ; 3 ; 4 5 6

-100 )t3 %? Xl
X

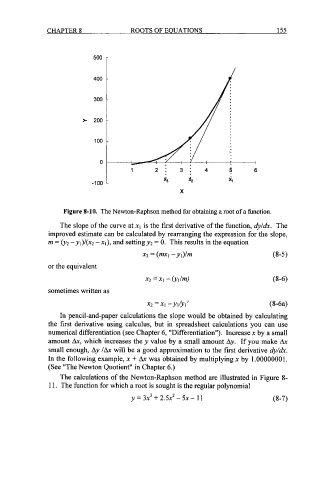
Figure 8-10. The Newton-Raphson method for obtaining a root of a function.

The slope of the curve at x1 is the first derivative of the function, dyldx. The
improved estimate can be calculated by rearranging the expression for the slope,
m = 0/2 -yl)/(x2 -XI), and settingy2 = 0. This results in the equation
x2 = -yJm (8-5)
or the equivalent

x2 = x1 - (yl/m) (8-6)
sometimes written as
x2 = XI - yl/yI ' (8-6a)
In pencil-and-paper calculations the slope would be obtained by calculating
the first derivative using calculus, but in spreadsheet calculations you can use
numerical differentiation (see Chapter 6, "Differentiation"). Increase x by a small
amount Ax, which increases the y value by a small amount Ay. If you make Ax
small enough, Ay /h will be a good approximation to the first derivative dy/dx.
In the following example, x + Ax was obtained by multiplying x by 1.00000001.
(See "The Newton Quotient'' in Chapter 6.)
The calculations of the Newton-Raphson method are illustrated in Figure 8-
1 1. The function for which a root is sought is the regular polynomial
y= 3x3 + 2.5~2- 5x- 11 (8-7)