Page 174 - Excel for Scientists and Engineers: Numerical Methods
P. 174
CHAPTER 8 ROOTS OF EQUATIONS I51
The Interval Method with Linear Interpolation
(the Regula Falsi Method)
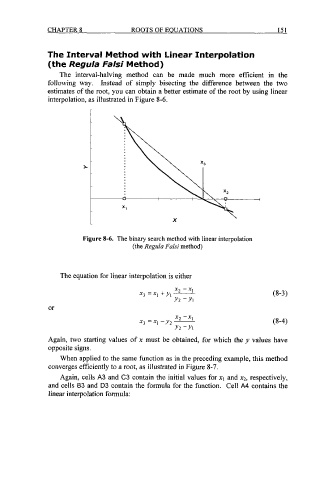
The interval-halving method can be made much more efficient in the
following way. Instead of simply bisecting the difference between the two
estimates of the root, you can obtain a better estimate of the root by using linear
interpolation, as illustrated in Figure 8-6.
1 X
Figure 8-6. The binary search method with linear interpolation
(the Regzila Falsi method)
The equation for linear interpolation is either
x2 -XI
xg =XI + y1 ___ (8-3)
Y2 -Y1
or
Again, two starting values of x must be obtained, for which the y values have
opposite signs.
When applied to the same hnction as in the preceding example, this method
converges efficiently to a root, as illustrated in Figure 8-7.
Again, cells A3 and C3 contain the initial values for XI and x2, respectively,
and cells 83 and 03 contain the formula for the function. Cell A4 contains the
linear interpolation formula: