Page 341 - Fiber Bragg Gratings

318 Chapter 7 Chirped Fiber Bragg Gratings

reflection, transmission, and group-delay response (see Chapter 4), in the
following we use the TMM approach to evaluate the transfer characteris-
tics of arbitrarily chirped gratings. There are naturally limitations to the
application of the TMM. Since coupled mode analysis depends on the slow
variation of the parameters of the grating as a function of the wavelength
of light, e.g., chirp, refractive index modulation, and coupling constant
K ac, it is not possible to compute entirely "arbitrary" gratings (see Chapter
4, Grating Simulation). Apart from this limitation, there are other ques-
tions that need addressing: for example, in the synthesis of chirped fiber
Bragg gratings, what constitutes a continuous chirp in view of the fact
that most gratings exhibit quasi-continuous chirp, and the influence of
apodization on the dispersion and reflection characteristics. First it is
necessary to view the grating as a physical entity, in which coupling
parameters are a weak function of space. Thus, it may be seen that a
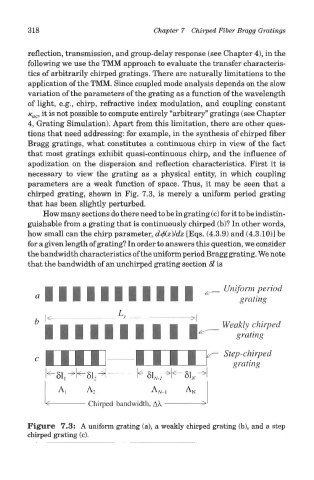
chirped grating, shown in Fig. 7.3, is merely a uniform period grating
that has been slightly perturbed.
How many sections do there need to be in grating (c) for it to be indistin-
guishable from a grating that is continuously chirped (b)? In other words,
how small can the chirp parameter, d(ft,z)/dz [Eqs. (4.3.9) and (4.3.10)3 be
for a given length of grating? In order to answers this question, we consider
the bandwidth characteristics of the uniform period Bragg grating. We note
that the bandwidth of an unchirped grating section SI is

Figure 7.3: A uniform grating (a), a weakly chirped grating (b), and a step
chirped grating (c).