Page 352 - Fiber Bragg Gratings

7.2 Chirped and step-chirped gratings 329

a peak reflectivity of—90% and are 100 mm long with a bandwidth of 0.75
nm (D g = ~1310 psec/nm), designed for compensation of the dispersion of
80 km of standard telecommunications fiber (D f =17 psec/nm/km). The
group delays have two features in common: The dispersion curves deviate
from linearity slowly across the bandwidth of the grating, and they are flat
within ±5 psec. With higher-reflectivity gratings, the curvature worsens.
Note, however, that the stronger, raised cosine apodization eliminates the
delay ripple almost entirely, but reduces the available bandwidth. Roman
and Winnick [44] have shown that using Gel'fand-Levitan-Marchenko
inverse scattering analysis, it is possible to design a grating with a near
perfect amplitude and quadratic phase response to recompress transform
limited pulses.
With asymmetric apodization as shown in Figs. 7.11 and 7.12, apodiz-
ing only one end of the grating has a beneficial effect of better bandwidth
utilization than symmetrically apodized gratings, since less of the grating
length is used in the apodization process. There is a slight increase in
the peak-to-peak group delay ripple on the long-wavelength side, as seen
in Fig. 7.12, but it is still <5 psec over a wider bandwidth. With a stronger
coupling constant and a different apodization function (e.g., tanh), we
note that less of the light reaches the rear end of the grating, so that the
ripple reduces still further. However, the curvature also increases. Figure
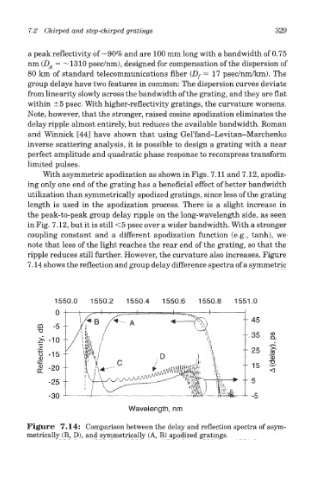
7.14 shows the reflection and group delay difference spectra of a symmetric

Figure 7.14: Comparison between the delay and reflection spectra of asym-
metrically (B, D), and symmetrically (A, B) apodized gratings.