Page 167 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: LINEAR DYNAMICS I 149

3.5.7 The effect of an elastic foundation

Interest in the subject arises, in part, because of Smith & Henmann’s (1972) unexpected
finding that for a cantilevered beam with a follower load the critical load (for coupled-
mode flutter) is independent of the foundation modulus. This corresponds to the pipe
system with /3 = 0.
#
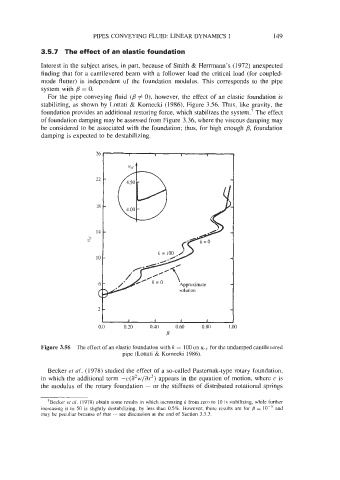
For the pipe conveying fluid (#I 0), however, the effect of an elastic foundation is
stabilizing, as shown by Lottati & Kornecki (1986), Figure 3.56. Thus, like gravity, the
foundation provides an additional restoring force, which stabilizes the system.+ The effect
of foundation damping may be assessed from Figure 3.36, where the viscous damping may
be considered to be associated with the foundation; thus, for high enough /3, foundation
damping is expected to be destabilizing.

26 -
I I 1 1

-
22

18 -

14 -
- -
%

10 -

6-

-
2-
I 1 1 I J
0.0 0.20 0.40 0.60 0.80 1 .oo
P
Figure 3.56 The effect of an elastic foundation with k = 100 on ucf for the undamped cantilevered
pipe (Lottati & Kornecki 1986).

Becker et al. (1978) studied the effect of a so-called Pasternak-type rotary foundation.
in which the additional term -c(a’w/&*) appears in the equation of motion, where c is
the modulus of the rotary foundation - or the stiffness of distributed rotational springs

TBecker et nl. (1978) obtain some results in which increasing k from zero to 10 is stabilizing, while further
increasing it to 50 is slightly destabilizing, by less than 0.5%. However, these results are for B = IO-’ and
may be peculiar because of that - see discussion at the end of Section 3.5.3.