Page 106 - Formation Damage during Improved Oil Recovery Fundamentals and Applications

88 Thomas Russell et al.

For the rock with pore sizes distributed as f s (r s ) and pores distributed by
sizes as f p (r p ), the following estimate of the maximum retention function is:
" p 2 #
ð N ð N 1 ffiffiffi 2
3ωπμr U
hσ cr i U; γ; pH; Tð Þ 5 1 2 1 s
0 0 2 2F e γ; pH;Tð ÞH

1 2 φ φf p r p f s r s ðÞdr s dr p : (3.19)
c

3.2.2.2 Monolayer of multisized fine particles
The monolayer model restricts each pore to contain at most a single layer
of attached particles. For each of these particles, the torque balance can
be applied to determine individually whether each particle will detach.
The nuance in this model is that particles are no longer assumed to be of
the same size.
The equations for the acting forces (Eqs. (3.6, 3.7, 3.8, and 3.14))
show some form of particle size dependence. A particle with larger size
experiences larger drag and lifting forces as well as larger electrostatic and
gravitational forces. Thus, both the detaching and attaching torques
increase with increasing particle size. When evaluated, it can be shown
that the particle size has a stronger influence on the detaching torque
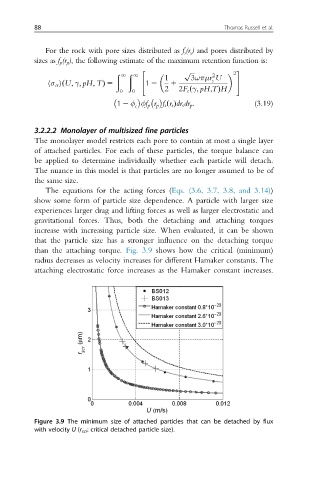
than the attaching torque. Fig. 3.9 shows how the critical (minimum)
radius decreases as velocity increases for different Hamaker constants. The
attaching electrostatic force increases as the Hamaker constant increases.

Figure 3.9 The minimum size of attached particles that can be detached by flux
with velocity U (r scr : critical detached particle size).