Page 152 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C003.fm Page 132 Monday, May 23, 2005 5:42 PM

132 Fracture Mechanics: Fundamentals and Applications

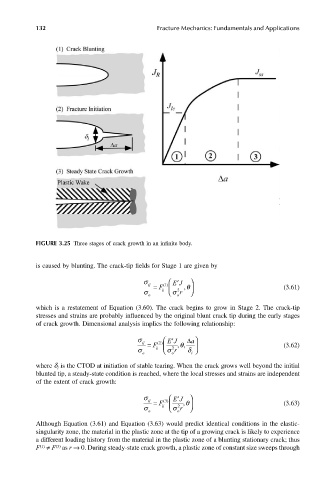
FIGURE 3.25 Three stages of crack growth in an infinite body.

is caused by blunting. The crack-tip fields for Stage 1 are given by
σ ij ()  EJ 
′
1
σ o = F ij   σ 2 o r θ ,   (3.61)

which is a restatement of Equation (3.60). The crack begins to grow in Stage 2. The crack-tip
stresses and strains are probably influenced by the original blunt crack tip during the early stages
of crack growth. Dimensional analysis implies the following relationship:
σ ij ()  EJ ∆ a 
′
2
σ o = F ij   σ 2 o r θ ,, δ   (3.62)
i
where d is the CTOD at initiation of stable tearing. When the crack grows well beyond the initial
i
blunted tip, a steady-state condition is reached, where the local stresses and strains are independent
of the extent of crack growth:
σ ij ()  EJ 
′
3
σ o = F ij   σ o 2 r θ ,   (3.63)

Although Equation (3.61) and Equation (3.63) would predict identical conditions in the elastic-
singularity zone, the material in the plastic zone at the tip of a growing crack is likely to experience
a different loading history from the material in the plastic zone of a blunting stationary crack; thus
(1)
(3)
F ≠ F as r → 0. During steady-state crack growth, a plastic zone of constant size sweeps through