Page 282 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C006.fm Page 262 Monday, May 23, 2005 5:50 PM

262 Fracture Mechanics: Fundamentals and Applications

(a)

(b)

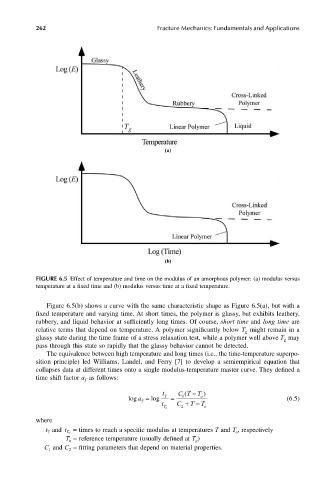
FIGURE 6.5 Effect of temperature and time on the modulus of an amorphous polymer: (a) modulus versus
temperature at a fixed time and (b) modulus versus time at a fixed temperature.

Figure 6.5(b) shows a curve with the same characteristic shape as Figure 6.5(a), but with a
fixed temperature and varying time. At short times, the polymer is glassy, but exhibits leathery,
rubbery, and liquid behavior at sufficiently long times. Of course, short time and long time are
relative terms that depend on temperature. A polymer significantly below T might remain in a
g
glassy state during the time frame of a stress relaxation test, while a polymer well above T may
g
pass through this state so rapidly that the glassy behavior cannot be detected.
The equivalence between high temperature and long times (i.e., the time-temperature superpo-
sition principle) led Williams, Landel, and Ferry [7] to develop a semiempirical equation that
collapses data at different times onto a single modulus-temperature master curve. They defined a
time shift factor a as follows:
T
t CT T )
( −
log a = T log T = 1 o (6.5)
t
T o C 2 T + T − o
where
= times to reach a specific modulus at temperatures T and T , respectively
t and t T o o
T
T = reference temperature (usually defined at T )
g
o
C and C = fitting parameters that depend on material properties.
1 2