Page 46 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C02.fm Page 26 Thursday, April 14, 2005 6:28 PM

26 Fracture Mechanics: Fundamentals and Applications

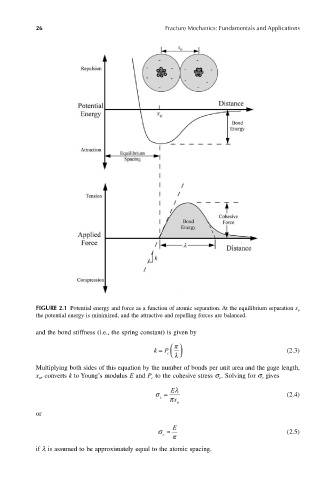
FIGURE 2.1 Potential energy and force as a function of atomic separation. At the equilibrium separation x o
the potential energy is minimized, and the attractive and repelling forces are balanced.

and the bond stiffness (i.e., the spring constant) is given by

π
k P = c   (2.3)
 
λ
Multiplying both sides of this equation by the number of bonds per unit area and the gage length,
x , converts k to Young’s modulus E and P to the cohesive stress σ . Solving for σ gives
c
c
c
o
E λ
σ = πx o (2.4)
c
or
E
σ ≈ π (2.5)
c
if λ is assumed to be approximately equal to the atomic spacing.