Page 165 - Fundamentals of Enhanced Oil and Gas Recovery

153
Thermal Recovery Processes

1.0

0.8 a(t–t ) i 4a(t–t ) i
V : θ = r h 2 V : θ = h 1 2
z
r
0.6
V V – (Single sand)
z
0.4
0.2 V r
0
0.01 0.1 1.0 10 10C
θ – Dimensionless time
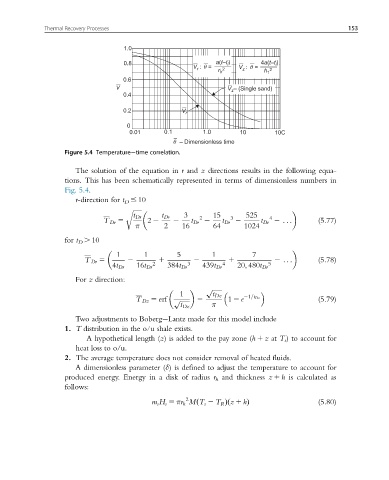
Figure 5.4 Temperature time correlation.

The solution of the equation in r and z directions results in the following equa-
tions. This has been schematically represented in terms of dimensionless numbers in
Fig. 5.4.
r-direction for t D # 10
r

ffiffiffiffiffiffi
3 15 525
t Dr t Dr 2 3 4
T Dr 5 2 2 2 t Dr 2 t Dr 2 t Dr 2 .. . (5.77)
π 2 16 64 1024
for t D . 10

1 1 5 1 7
T Dr 5 2 1 2 1 2 .. . (5.78)
2 3 4 5
4t Dr 16t Dr 384t Dr 439t Dr 20; 480t Dr
For z direction:
p
ffiffiffiffiffiffi
1 t Dz
T Dz 5 erf p ffiffiffiffiffiffi 2 1 2 e 21=t Dz (5.79)
t Dz π
Two adjustments to Boberg Lantz made for this model include
1. T distribution in the o/u shale exists.
A hypothetical length (z) is added to the pay zone (h 1 z at T s ) to account for
heat loss to o/u.
2. The average temperature does not consider removal of heated fluids.
A dimensionless parameter (δ) is defined to adjust the temperature to account for
produced energy. Energy in a disk of radius r h and thickness z 1 h is calculated as
follows:

2
m s H s 5 πr h MT s 2 T R Þðz 1 hÞ (5.80)
ð