Page 60 - Fundamentals of Physical Volcanology

9780632054435_4_003.qxd 12/10/2007 12:18PM Page 37

MAGMA MIGRATION 37

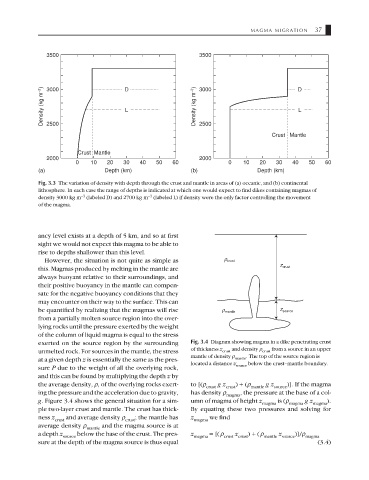
3500 3500

Density (kg m –3 ) 3000 D Density (kg m –3 ) 3000 D

L
L
2500
2500
Crust Mantle

Crust Mantle
2000 2000
0 10 20 30 40 50 60 0 10 20 30 40 50 60
(a) Depth (km) (b) Depth (km)
Fig. 3.3 The variation of density with depth through the crust and mantle in areas of (a) oceanic, and (b) continental
lithosphere. In each case the range of depths is indicated at which one would expect to find dikes containing magmas of
−3
−3
density 3000 kg m (labeled D) and 2700 kg m (labeled L) if density were the only factor controlling the movement
of the magma.

ancy level exists at a depth of 5 km, and so at first
sight we would not expect this magma to be able to
rise to depths shallower than this level.
However, the situation is not quite as simple as ρ
ρ crust
this. Magmas produced by melting in the mantle are z crust
always buoyant relative to their surroundings, and
their positive buoyancy in the mantle can compen-
sate for the negative buoyancy conditions that they

may encounter on their way to the surface. This can
be quantified by realizing that the magmas will rise ρ z source
ρ mantle
from a partially molten source region into the over-
lying rocks until the pressure exerted by the weight
of the column of liquid magma is equal to the stress
exerted on the source region by the surrounding Fig. 3.4 Diagram showing magma in a dike penetrating crust
unmelted rock. For sources in the mantle, the stress of thickness z crust and density ρ crust from a source in an upper
mantle of density ρ . The top of the source region is
at a given depth z is essentially the same as the pres- mantle
located a distance z below the crust–mantle boundary.
sure P due to the weight of all the overlying rock, source
and this can be found by multiplying the depth z by
the average density, ρ, of the overlying rocks exert- to [(ρ crust gz crust ) + (ρ mantle gz source )]. If the magma
ing the pressure and the acceleration due to gravity, has density ρ , the pressure at the base of a col-
magma
g. Figure 3.4 shows the general situation for a sim- umn of magma of height z is (ρ gz ).
magma magma magma
ple two-layer crust and mantle. The crust has thick- By equating these two pressures and solving for
ness z crust and average density ρ crust ; the mantle has z magma we find
average density ρ and the magma source is at
mantle
a depth z below the base of the crust. The pres- z = [(ρ z ) + (ρ z )]/ρ
source magma crust crust mantle source magma
sure at the depth of the magma source is thus equal (3.4)