Page 290 - Fundamentals of Probability and Statistics for Engineers

Parameter Estimation 273

∧ ∧
∧ (θ 2 ) f Θ 2 (θ 2 )
∧
f Θ 2

∧
∧ (θ 1 ) ∧
∧ (θ 1 )
f Θ 1
f Θ 1

θ ∧∧ θ ∧∧
θ 1 ,θ 2
θ 1 ,θ 2
(a) (b)
^
^
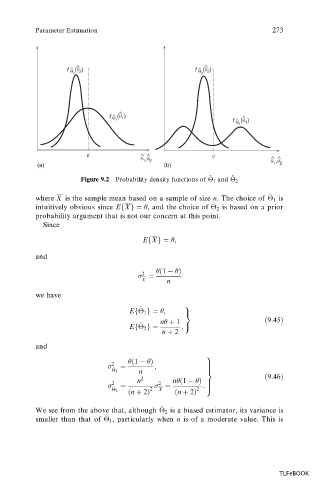
Figure 9.2 Probability density functions of 1 and 2
^
where X is the sample mean based on a sample of size n. The choice of 1 is
^
intuitively obvious since EfXgˆ , and the choice of 2 is based on a prior
probability argument that is not our concern at this point.
Since
EfXgˆ ;

and
1 †
2
ˆ
X n
we have

^
Ef 1 gˆ ; 9
=
n ‡ 1 9:45†
^
Ef 2 gˆ ; ;
n ‡ 2
and
9
1 †
2 ˆ ; >
>
n
^ 1 >
=
n 2 9:46†
2
2 ˆ ˆ n 1 † >
>
: >
^ 2 2 X 2 ;
n ‡ 2† n ‡ 2†
^
We see from the above that, although 2 is a biased estimator, its variance is
^
smaller than that of 1 , particularly when n is of a moderate value. This is

TLFeBOOK