Page 247 - Fundamentals of Radar Signal Processing

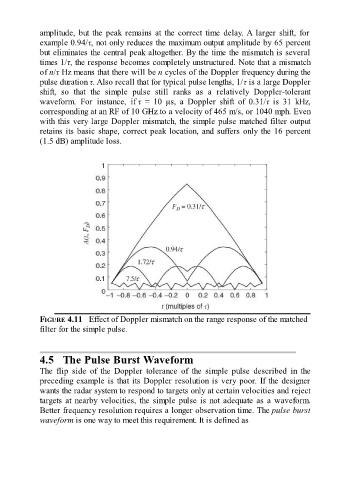
amplitude, but the peak remains at the correct time delay. A larger shift, for

example 0.94/τ, not only reduces the maximum output amplitude by 65 percent
but eliminates the central peak altogether. By the time the mismatch is several
times 1/τ, the response becomes completely unstructured. Note that a mismatch
of n/τ Hz means that there will be n cycles of the Doppler frequency during the
pulse duration τ. Also recall that for typical pulse lengths, 1/τ is a large Doppler
shift, so that the simple pulse still ranks as a relatively Doppler-tolerant

waveform. For instance, if τ = 10 μs, a Doppler shift of 0.31/τ is 31 kHz,
corresponding at an RF of 10 GHz to a velocity of 465 m/s, or 1040 mph. Even
with this very large Doppler mismatch, the simple pulse matched filter output
retains its basic shape, correct peak location, and suffers only the 16 percent
(1.5 dB) amplitude loss.

FIGURE 4.11 Effect of Doppler mismatch on the range response of the matched
filter for the simple pulse.

4.5 The Pulse Burst Waveform

The flip side of the Doppler tolerance of the simple pulse described in the
preceding example is that its Doppler resolution is very poor. If the designer
wants the radar system to respond to targets only at certain velocities and reject
targets at nearby velocities, the simple pulse is not adequate as a waveform.
Better frequency resolution requires a longer observation time. The pulse burst
waveform is one way to meet this requirement. It is defined as