Page 315 - Fundamentals of Reservoir Engineering

REAL GAS FLOW: GAS WELL TESTING 250

m (p)
p - from material balance
Z
m ( )
p
p

p
m ( ) p p

1422 QT r 3
p
m (p ) = m ( ) − ln e − + S
wf
kh r w 4
m (p)

m (p )
wf

m (p )
wf

p wf p wf p

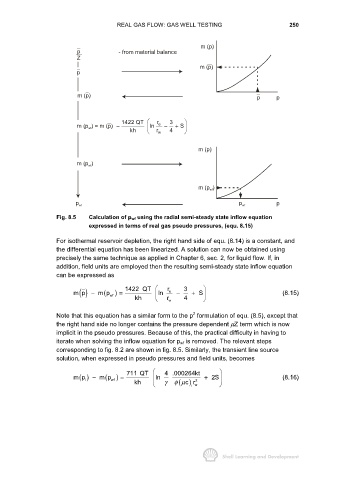
Fig. 8.5 Calculation of p wf using the radial semi-steady state inflow equation
expressed in terms of real gas pseudo pressures, (equ. 8.15)

For isothermal reservoir depletion, the right hand side of equ. (8.14) is a constant, and
the differential equation has been linearized. A solution can now be obtained using
precisely the same technique as applied in Chapter 6, sec. 2, for liquid flow. If, in
addition, field units are employed then the resulting semi-steady state inflow equation
can be expressed as
1422 QT r 3
mp mp ) = ln e − + S (8.15)
(
() −
wf
kh r w 4
2
Note that this equation has a similar form to the p formulation of equ. (8.5), except that
the right hand side no longer contains the pressure dependent µZ term which is now
implicit in the pseudo pressures. Because of this, the practical difficulty in having to
iterate when solving the inflow equation for p wf is removed. The relevant steps
corresponding to fig. 8.2 are shown in fig. 8.5. Similarly, the transient line source
solution, when expressed in pseudo pressures and field units, becomes

711 QT 4 .000264kt
mp mp ) = ln + 2S (8.16)
(
() −
wf
i
kh γ φ µ i w 2
( ) c r