Page 49 - Geothermal Energy Renewable Energy and The Environment

32 Geothermal Energy: Renewable Energy and the Environment

changes in the state parameters, P and T. If the conditions to which the system is subject to change,
either by moving heat (q) into it or by doing work (w) on it, the internal energy E must also change.
The mathematical statement of this process is
Δ E = E – E ,
f
i
which states that the change in internal energy (ΔE) is equal to the internal energy of the system in
its final state (E ) minus the initial internal energy (E).
f
i
This simple equation is profoundly important. It establishes the significance of knowing the
internal energy at the end points of a process that affects a system. It is the difference between these
end points that determines how much energy is available to heat a space, generate power, or cool a
room. It also emphasizes that the pathway that was followed to get from the initial to the final states
has no significance for the change in internal energy. For example, imagine a volume of gas con-
tained in a cylinder and that the cylinder is a perfect insulator, not allowing heat to be added to or
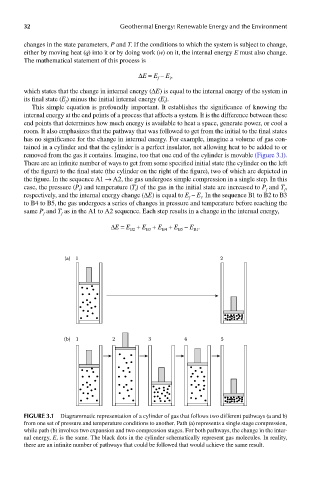
removed from the gas it contains. Imagine, too that one end of the cylinder is movable (Figure 3.1).
There are an infinite number of ways to get from some specified initial state (the cylinder on the left
of the figure) to the final state (the cylinder on the right of the figure), two of which are depicted in
the figure. In the sequence A1 → A2, the gas undergoes simple compression in a single step. In this
case, the pressure (P) and temperature (T) of the gas in the initial state are increased to P and T ,
i
i
f
f
respectively, and the internal energy change (ΔE) is equal to E – E . In the sequence B1 to B2 to B3
f
i
to B4 to B5, the gas undergoes a series of changes in pressure and temperature before reaching the
same P and T as in the A1 to A2 sequence. Each step results in a change in the internal energy,
f
f
Δ E = E + E + E + E – E .
B4
B1
B5
B2
B3
(a) 1 2

(b) 1 2 3 4 5

FIGUre 3.1 Diagrammatic representation of a cylinder of gas that follows two different pathways (a and b)
from one set of pressure and temperature conditions to another. Path (a) represents a single stage compression,
while path (b) involves two expansion and two compression stages. For both pathways, the change in the inter-
nal energy, E, is the same. The black dots in the cylinder schematically represent gas molecules. In reality,
there are an infinite number of pathways that could be followed that would achieve the same result.