Page 244 - Geology and Geochemistry of Oil and Gas
P. 244
MODELS OF STATIC GEOLOGIC SYSTEMS 211
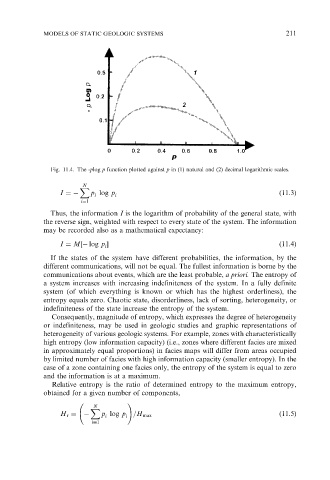
Fig. 11.4. The -plog p function plotted against p in (1) natural and (2) decimal logarithmic scales.
N
X
I ¼ p log p (11.3)
i i
i¼1
Thus, the information I is the logarithm of probability of the general state, with
the reverse sign, weighted with respect to every state of the system. The information
may be recorded also as a mathematical expectancy:
I ¼ M½ log p (11.4)
i
If the states of the system have different probabilities, the information, by the
different communications, will not be equal. The fullest information is borne by the
communications about events, which are the least probable, a priori. The entropy of
a system increases with increasing indefiniteness of the system. In a fully definite
system (of which everything is known or which has the highest orderliness), the
entropy equals zero. Chaotic state, disorderliness, lack of sorting, heterogeneity, or
indefiniteness of the state increase the entropy of the system.
Consequently, magnitude of entropy, which expresses the degree of heterogeneity
or indefiniteness, may be used in geologic studies and graphic representations of
heterogeneity of various geologic systems. For example, zones with characteristically
high entropy (low information capacity) (i.e., zones where different facies are mixed
in approximately equal proportions) in facies maps will differ from areas occupied
by limited number of facies with high information capacity (smaller entropy). In the
case of a zone containing one facies only, the entropy of the system is equal to zero
and the information is at a maximum.
Relative entropy is the ratio of determined entropy to the maximum entropy,
obtained for a given number of components,
!
N
X
H r ¼ p log p i =H max (11.5)
i
i¼1