Page 483 - Handbook Of Integral Equations

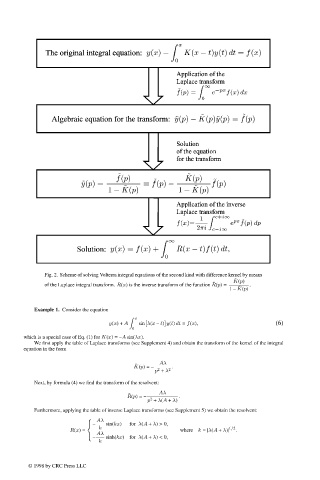
Fig. 2. Scheme of solving Volterra integral equations of the second kind with difference kernel by means
˜ K(p)
of the Laplace integral transform. R(x) is the inverse transform of the function ˜ R(p)= .
1 – ˜ K(p)

Example 1. Consider the equation
x

y(x)+ A sin λ(x – t) y(t) dt = f(x), (6)
0
which is a special case of Eq. (1) for K(x)= –A sin(λx).
We first apply the table of Laplace transforms (see Supplement 4) and obtain the transform of the kernel of the integral
equation in the form
Aλ
˜ K(p)= – .
2
p + λ 2
Next, by formula (4) we find the transform of the resolvent:
Aλ
˜ R(p)= – .
2
p + λ(A + λ)
Furthermore, applying the table of inverse Laplace transforms (see Supplement 5) we obtain the resolvent:
Aλ

 – sin(kx) for λ(A + λ)>0,

R(x)= k where k = |λ(A + λ)| 1/2 .
 Aλ
 – sinh(kx) for λ(A + λ)<0,
k
© 1998 by CRC Press LLC

© 1998 by CRC Press LLC
Page 465