Page 494 - Handbook Of Integral Equations

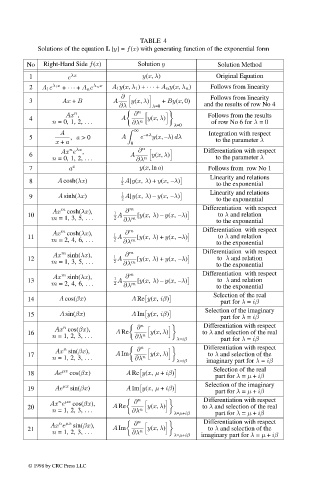
TABLE 4
Solutions of the equation L [y]= f(x) with generating function of the exponential form

No Right-Hand Side f(x) Solution y Solution Method
1 e λx y(x, λ) Original Equation
2 A 1 e λ 1 x + ··· + A n e λ n x A 1 y(x, λ 1 )+ ··· + A n y(x, λ n ) Follows from linearity
∂ Follows from linearity
3 Ax + B A y(x, λ) + By(x,0)
∂λ λ=0 and the results of row No 4
n ∂ n
Ax , Follows from the results
4 A y(x, λ)
n = 0,1,2, ... ∂λ n of row No 6 for λ =0
λ=0
A ∞ –aλ Integration with respect
5 , a >0 A e y(x, –λ) dλ
x + a 0 to the parameter λ
n λx
Ax e , ∂ n Differentiation with respect
6 A y(x, λ)
n = 0,1,2, ... ∂λ n to the parameter λ
7 a x y(x,ln a) Follows from row No 1
8 A cosh(λx) 1 A[y(x, λ)+ y(x, –λ) Linearity and relations
2 to the exponential
Linearity and relations

1
9 A sinh(λx) A[y(x, λ) – y(x, –λ)
2 to the exponential
m
Ax cosh(λx), 1 ∂ m Differentiation with respect
10 A [y(x, λ) – y(x, –λ) to λ and relation
m = 1,3,5, ... 2 ∂λ m to the exponential
m
Ax cosh(λx), 1 ∂ m Differentiation with respect
11 A [y(x, λ)+ y(x, –λ) to λ and relation
m = 2,4,6, ... 2 ∂λ m to the exponential
m
Ax sinh(λx), 1 ∂ m Differentiation with respect
12 A [y(x, λ)+ y(x, –λ) to λ and relation
m = 1,3,5, ... 2 ∂λ m to the exponential
m
Ax sinh(λx), 1 ∂ m Differentiation with respect
13 A [y(x, λ) – y(x, –λ) to λ and relation
m = 2,4,6, ... 2 ∂λ m to the exponential
Selection of the real
14 A cos(βx) A Re y(x, iβ)
part for λ = iβ
Selection of the imaginary
15 A sin(βx) A Im y(x, iβ)
part for λ = iβ
n Differentiation with respect
n
Ax cos(βx), ∂
16 A Re y(x, λ) to λ and selection of the real
n = 1,2,3, ... ∂λ n
λ=iβ part for λ = iβ
n Differentiation with respect
n
Ax sin(βx), ∂
17 A Im y(x, λ) to λ and selection of the
n = 1,2,3, ... ∂λ n
λ=iβ imaginary part for λ = iβ

18 Ae µx cos(βx) A Re y(x, µ + iβ) Selection of the real
part for λ = µ + iβ

19 Ae µx sin(βx) A Im y(x, µ + iβ) Selection of the imaginary
part for λ = µ + iβ
n Differentiation with respect
n µx
Ax e cos(βx), ∂
20 A Re n y(x, λ) to λ and selection of the real
n = 1,2,3, ... ∂λ
λ=µ+iβ part for λ = µ + iβ
n Differentiation with respect
n µx
Ax e sin(βx), ∂
21 A Im n y(x, λ) to λ and selection of the
n = 1,2,3, ... ∂λ
λ=µ+iβ imaginary part for λ = µ + iβ
© 1998 by CRC Press LLC

© 1998 by CRC Press LLC
Page 476