Page 111 - Handbook of Biomechatronics

Model-Based Control of Biomechatronic Systems 107

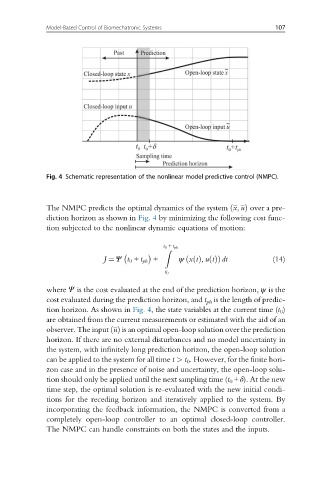
Fig. 4 Schematic representation of the nonlinear model predictive control (NMPC).

The NMPC predicts the optimal dynamics of the system x, uÞ over a pre-
ð
diction horizon as shown in Fig. 4 by minimizing the following cost func-
tion subjected to the nonlinear dynamic equations of motion:

t 0 + t ph
Z

J ¼ Ψ t 0 + t ph + ψ xtðÞ, utðÞÞ dt (14)
ð
t 0
where Ψ is the cost evaluated at the end of the prediction horizon, ψ is the
cost evaluated during the prediction horizon, and t ph is the length of predic-
tion horizon. As shown in Fig. 4, the state variables at the current time (t 0 )
are obtained from the current measurements or estimated with the aid of an
observer. The input uðÞ is an optimal open-loop solution over the prediction
horizon. If there are no external disturbances and no model uncertainty in
the system, with infinitely long prediction horizon, the open-loop solution
can be applied to the system for all time t > t 0 . However, for the finite hori-
zon case and in the presence of noise and uncertainty, the open-loop solu-
tion should only be applied until the next sampling time (t 0 +δ). At the new
time step, the optimal solution is re-evaluated with the new initial condi-
tions for the receding horizon and iteratively applied to the system. By
incorporating the feedback information, the NMPC is converted from a
completely open-loop controller to an optimal closed-loop controller.
The NMPC can handle constraints on both the states and the inputs.