Page 511 - Handbook of Biomechatronics

Bioinspired and Biomimetic Micro-Robotics for Therapeutic Applications 505

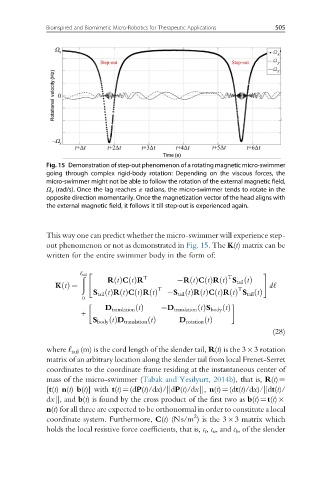
Fig. 15 Demonstration of step-out phenomenon of a rotating magnetic micro-swimmer
going through complex rigid-body rotation: Depending on the viscous forces, the
micro-swimmer might not be able to follow the rotation of the external magnetic field,
Ω x (rad/s). Once the lag reaches π radians, the micro-swimmer tends to rotate in the
opposite direction momentarily. Once the magnetization vector of the head aligns with
the external magnetic field, it follows it till step-out is experienced again.

This way one can predict whether the micro-swimmer will experience step-
out phenomenon or not as demonstrated in Fig. 15. The K(t) matrix can be
written for the entire swimmer body in the form of:

ð tail
‘ " #
T T
R tðÞC tðÞR tðÞ S tail tðÞ
R tðÞC tðÞR
K tðÞ ¼ T T d‘
S tail tðÞR tðÞC tðÞR tðÞ S tail tðÞR tðÞC tðÞR tðÞ S tail tðÞ
0

D translation tðÞ D translation tðÞS body tðÞ
+
S body tðÞD translation tðÞ D rotation tðÞ
(28)
where ‘ tail (m) is the cord length of the slender tail, R(t) is the 3 3 rotation
matrix of an arbitrary location along the slender tail from local Frenet-Serret
coordinates to the coordinate frame residing at the instantaneous center of
mass of the micro-swimmer (Tabak and Yesilyurt, 2014b), that is, R(t)¼
[t(t) n(t) b(t)] with t(t)¼(dP(t)/dx)/jjdP(t)/dxjj, n(t)¼(dt(t)/dx)/jjdt(t)/
dxjj, and b(t) is found by the cross product of the first two as b(t)¼t(t)
n(t) for all three are expected to be orthonormal in order to constitute a local
2
coordinate system. Furthermore, C(t) (Ns/m ) is the 3 3 matrix which
holds the local resistive force coefficients, that is, c t , c n , and c b , of the slender