Page 214 - Handbook of Plastics Technologies

ELASTOMERS

4.6 CHAPTER 4

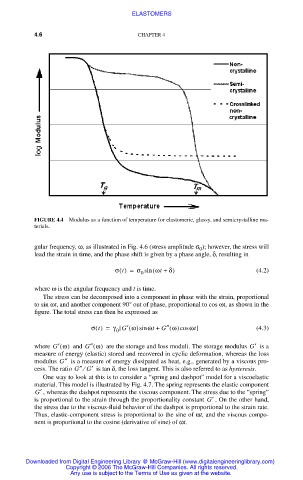
FIGURE 4.4 Modulus as a function of temperature for elastomeric, glassy, and semicrystalline ma-
terials.

gular frequency, ω, as illustrated in Fig. 4.6 (stress amplitude σ ); however, the stress will
0
lead the strain in time, and the phase shift is given by a phase angle, δ, resulting in
σ t() = σ sin ( ωt + δ) (4.2)
0
where ω is the angular frequency and t is time.
The stress can be decomposed into a component in phase with the strain, proportional
to sin ωt, and another component 90° out of phase, proportional to cos ωt, as shown in the
figure. The total stress can then be expressed as

σ t() = γ G′ω()sin[ ωt + G″ω()cos ωt] (4.3)
0
where G′ω() and G″ω() are the storage and loss moduli. The storage modulus G′ is a
measure of energy (elastic) stored and recovered in cyclic deformation, whereas the loss
modulus G″ is a measure of energy dissipated as heat, e.g., generated by a viscous pro-
cess. The ratio G″ G′⁄ is tan δ, the loss tangent. This is also referred to as hysteresis.
One way to look at this is to consider a “spring and dashpot” model for a viscoelastic
material. This model is illustrated by Fig. 4.7. The spring represents the elastic component
G′ , whereas the dashpot represents the viscous component. The stress due to the “spring”
is proportional to the strain through the proportionality constant G′ . On the other hand,
the stress due to the viscous-fluid behavior of the dashpot is proportional to the strain rate.
Thus, elastic-component stress is proportional to the sine of ωt, and the viscous compo-
nent is proportional to the cosine (derivative of sine) of ωt.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2006 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.