Page 437 - Handbook of Properties of Textile and Technical Fibres

410 Handbook of Properties of Textile and Technical Fibres

1 Irreversibly dissipated energy
800
2 Viscous energy dissipation
Stress (MPa) 400 (2) Second loading cycle (1) 1
600
Elastically stored energy
3
(1) First loading cycle
200 (2) (2) 2 3
(1)
0
0 0.04 0.08 0.12 0.16
Deformation (–)
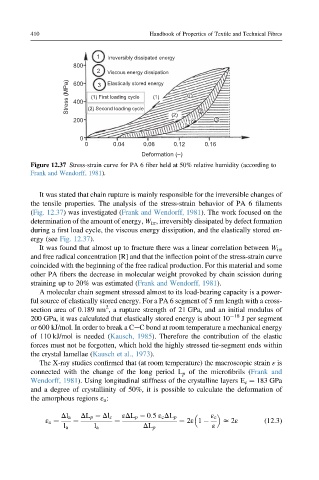
Figure 12.37 Stress-strain curve for PA 6 fiber held at 50% relative humidity (according to
Frank and Wendorff, 1981).

It was stated that chain rupture is mainly responsible for the irreversible changes of
the tensile properties. The analysis of the stress-strain behavior of PA 6 filaments
(Fig. 12.37) was investigated (Frank and Wendorff, 1981). The work focused on the
determination of the amount of energy, W irr , irreversibly dissipated by defect formation
during a first load cycle, the viscous energy dissipation, and the elastically stored en-
ergy (see Fig. 12.37).
It was found that almost up to fracture there was a linear correlation between W irr
and free radical concentration [R] and that the inflection point of the stress-strain curve
coincided with the beginning of the free radical production. For this material and some
other PA fibers the decrease in molecular weight provoked by chain scission during
straining up to 20% was estimated (Frank and Wendorff, 1981).
A molecular chain segment stressed almost to its load-bearing capacity is a power-
ful source of elastically stored energy. For a PA 6 segment of 5 nm length with a cross-
2
section area of 0.189 nm , a rupture strength of 21 GPa, and an initial modulus of
200 GPa, it was calculated that elastically stored energy is about 10 18 J per segment
or 600 kJ/mol. In order to break a CeC bond at room temperature a mechanical energy
of 110 kJ/mol is needed (Kausch, 1985). Therefore the contribution of the elastic
forces must not be forgotten, which hold the highly stressed tie-segment ends within
the crystal lamellae (Kausch et al., 1973).
The X-ray studies confirmed that (at room temperature) the macroscopic strain ε is
connected with the change of the long period L p of the microfibrils (Frank and
Wendorff, 1981). Using longitudinal stiffness of the crystalline layers E c ¼ 183 GPa
and a degree of crystallinity of 50%, it is possible to calculate the deformation of
the amorphous regions ε a :

Dl a DL p Dl c εDL p 0:5 ε c DL p ε c
ε a ¼ ¼ ¼ ¼ 2ε 1 z 2ε (12.3)
l a l a DL p ε