Page 162 - Hardware Implementation of Finite-Field Arithmetic

m
Operations over GF ( p ) 145

n_a(x) c(x) n_b(x) e(x)
n_b m
0 1 0 1 sel_sub
mod p
sub1(x) coef nbe(x) e (x)x e m–1 f (x) – x m n_a m inverter d (x)

mod p mod p
multipliers multipliers mod p mod p
sub3 (x)
sub2 (x) sub4(x) multiplier multipliers
mod p mod p
subtractors subtractors coef z(x)
out1(x) out 2(x) d(x)
deg_r
2 1 0 sel_e
deg_a e(x)
–1
n_r (x)x
deg_r – 1
register ce ce_e initially: ce ce_d
g(x)
0 1 0 1 sel_r
e (x) d (x)
register ce ce_r
deg_b
n_r (x) deg_r
–1
deg_r
n_b (x) n_r (x) deg_b deg_r n_b (x)x n_r (x) deg_b – 1 d(x ) e(x)

0 1 0 1 sel_a 0 1 0 1 sel_b 0 1 sel_a

initially: ce ce_a initially: ce ce_b initially: ce ce_a
f (x) m h(x)x m – 1 zero

n_a(x) deg_a n_b(x) deg_b c(x)
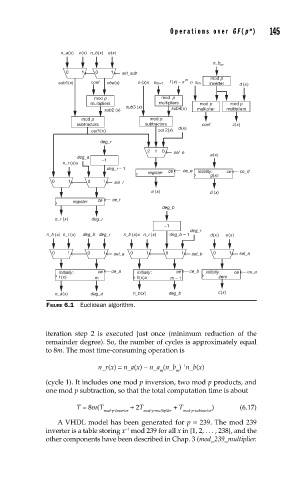
FIGURE 6.1 Euclidean algorithm.

iteration step 2 is executed just once (minimum reduction of the
remainder degree). So, the number of cycles is approximately equal
to 8m. The most time-consuming operation is

n_r(x) = n_a(x) − n_a (n_b ) n_b(x)
−1
m m
(cycle 1). It includes one mod p inversion, two mod p products, and
one mod p subtraction, so that the total computation time is about

T ≈ 8m(T + 2T + T ) (6.17)
mod-p-inverter mod-p-multiplier mod-p-subtractor
A VHDL model has been generated for p = 239. The mod 239
inverter is a table storing x mod 239 for all x in {1, 2, . . . , 238}, and the
−1
other components have been described in Chap. 3 (mod_239_multiplier.