Page 63 - Hardware Implementation of Finite-Field Arithmetic

46 Cha pte r T w o

Algorithm 2.9—Barrett reduction with B = 2
y := x(n-1..k-1); prod := y*c; q := prod(n+2..n-k+1);
prod := q*m; r := x(k+1..0) - prod(k+1..0);
while r >= m loop r := r-m; end loop;
z := r;
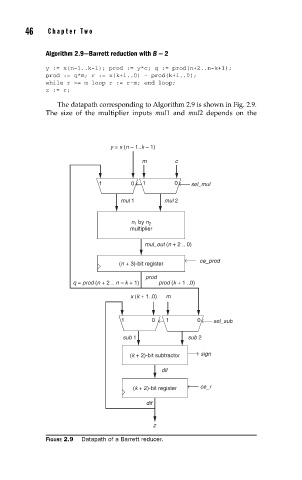
The datapath corresponding to Algorithm 2.9 is shown in Fig. 2.9.
The size of the multiplier inputs mul1 and mul2 depends on the

y = x (n – 1..k – 1)
m c

1 0 1 0 sel_mul

mul 1 mul 2

n 1 by n 2
multiplier
mul_out (n + 2 .. 0)

ce_prod
(n + 3)-bit register
prod
q = prod (n +2 .. n – k + 1) prod (k +1 ..0)
x (k + 1..0) m

1 0 1 0 sel_sub

sub 1 sub 2

(k + 2)-bit subtractor sign

dif

(k + 2)-bit register ce_r

dif

z

FIGURE 2.9 Datapath of a Barrett reducer.