Page 346 - High Temperature Solid Oxide Fuel Cells Fundamentals, Design and Applications

322 High Temperature Solid Oxide Fuel Cells: Fundamentals, Design and Applications

(a) Auode-Supported Cell

(b) Cathwle-Supported Cell
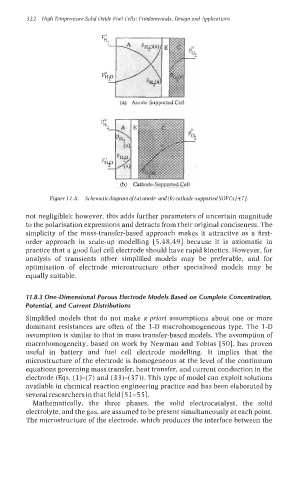
Figure I I .8. Schematicdiagram of(a)anode-and(b)cathode-supportedSOFCs[47].

not negligible); however, this adds further parameters of uncertain magnitude
to the polarisation expressions and detracts from their original conciseness. The
simplicity of the mass-transfer-based approach makes it attractive as a first-
order approach in scale-up modelling [5,48,49] because it is axiomatic in
practice that a good fuel cell electrode should have rapid kinetics. However, for
analysis of transients other simplified models may be preferable, and for
optimisation of electrode microstructure other specialised models may be
equally suitable.

11.8.3 One-Dimensional Porous Electrode Models Based on Complete Concentration,
Potential, and Current Distributions
Simplified models that do not make a priori assumptions about one or more
dominant resistances are often of the 1-D macrohomogeneous type. The 1-D
assumption is similar to that in mass transfer-based models. The assumption of
macrohomogeneity, based on work by Newman and Tobias [SO], has proven
useful in battery and fuel cell electrode modelling. It implies that the
microstructure of the electrode is homogeneous at the level of the continuum
equations governing mass transfer, heat transfer, and current conduction in the
electrode (Eqs. (1)-(7) and (33)-(37)). This type of model can exploit solutions
available in chemical reaction engineering practice and has been elaborated by
several researchers in that field [ 5 1-5 51.
Mathematically, the three phases, the solid electrocatalyst, the solid
electrolyte, and the gas, are assumed to be present simultaneously at each point.
The microstructure of the electrode, which produces the interface between the