Page 130 - How To Solve Word Problems In Calculus

A = xy.
y 12 − x
Since
ABC is similar to
ADE, = . It follows that
5 12
5
y = (12 − x), 0 ≤ x ≤ 12. (If x > 12, y < 0.)
12
The area, as a function of x, becomes
5
A(x) = x · (12 − x)
12
5 2
= (12x − x )
12
Differentiating, we obtain
5

A (x) = (12 − 2x)
12
5
0 = (12 − 2x)
12
x = 6

Since A(0) = A(12) = 0, the maximum area occurs when x = 6 and
5 5 5
2
y = (12 − 6) = . The maximum area = xy = 6 · = 15 in .
12 2 2
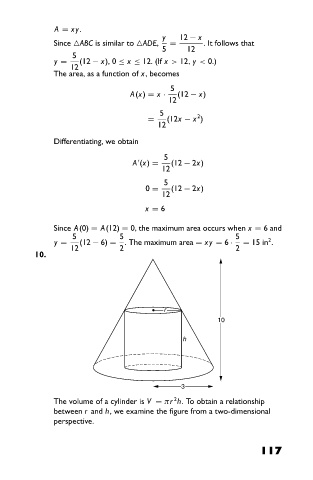
10.

r
10

h

3
2
The volume of a cylinder is V = πr h. To obtain a relationship
between r and h, we examine the figure from a two-dimensional
perspective.

117