Page 206 - How To Solve Word Problems In Calculus

P1: FYN/FZQ P2: FXS
PB056-07 Macros-FMT June 1, 2001 13:49 Char Count= 0

2
5. Find the area of the region bounded by the curves 4x − y = 0 and
y = 2x − 4.
2
6. Find the area of the region bounded by the parabola y = x , the
tangent line to the parabola at the point (2, 4), and the x axis.
7. Derive a formula for the volume of a sphere of radius r by rotating
√
2
2
the semicircle y = r − x about the x axis.
8. Compute the volume of the solid obtained by rotating the region
2
2
bounded by y = x , y = 8 − x , and the y axis about the x axis.
9. A hole of radius 2 is drilled through the axis of a sphere of radius 3.
Compute the volume of the remaining solid.
Solutions to Supplementary Problems

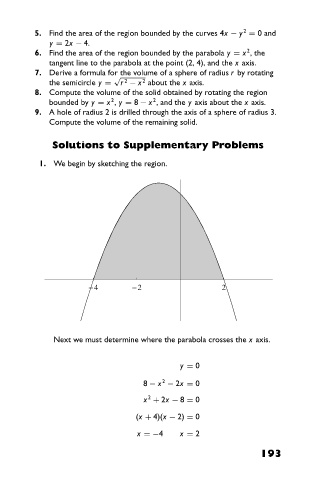
1. We begin by sketching the region.

− 4 − 2 2 2
−2
−4

Next we must determine where the parabola crosses the x axis.

y = 0

2
8 − x − 2x = 0
2
x + 2x − 8 = 0
(x + 4)(x − 2) = 0

x =−4 x = 2

193